
分析 利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,求得n的最小值.
解答 解:为了得到y=cos(2πx-$\frac{π}{3}$)=sin(2πx-$\frac{π}{3}$+$\frac{π}{2}$)=sin(2πx+$\frac{π}{6}$)=sin2π(x+$\frac{1}{12}$)的图象,
只需将y=sin(2πx+$\frac{π}{3}$)=sin2π(x+$\frac{1}{6}$)的图象向右平移n(n>0)个单位,
则n的最小值为n=$\frac{1}{6}$-$\frac{1}{12}$=$\frac{1}{12}$,
故答案为:$\frac{1}{12}$.
点评 本题主要考查诱导公式,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
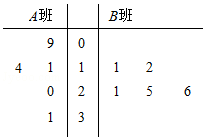 某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的抛物面围成的几何体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( )
抛物线y=x2(-2≤x≤2)绕y轴旋转一周形成一个如图所示的抛物面围成的几何体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com