
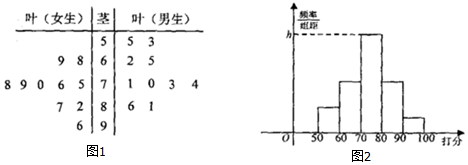
分析 (Ⅰ)利用茎叶图能求出女生打分的平均分和男生打分的平均分,从茎叶图来看,女生打分相对集中,男生打分相对分散.
(Ⅱ)20名学生中,打分区间[0,60)、[60,70)、[70,80)、[80,90)、[90,100]中的学生数分别为:2人,4人,9人,4人,1人,打分区间[70,80)的人数最多,有9人,所点频率为0.45,由此能求出最高矩形的高.
(Ⅲ)打分在70分以下(不含70分)的同学有6人,其中男生4人,女生2人,有女生被抽中的对立事件是抽中的3名同学都是男生,由此利用对立事件概率计算公式能求出有女生被抽中的概率.
解答 解:(Ⅰ)女生打分的平均分为:
$\overline{{x}_{1}}$=$\frac{1}{10}$(68+69+75+76+70+79+78+82+87+96)=78,
男生打分的平均分为:
$\overline{{x}_{2}}$=$\frac{1}{10}$(55+53+62+65+71+70+73+74+86+81)=69.
从茎叶图来看,女生打分相对集中,男生打分相对分散.
(Ⅱ)20名学生中,打分区间[0,60)、[60,70)、[70,80)、[80,90)、[90,100]中的学生数分别为:
2人,4人,9人,4人,1人,
打分区间[70,80)的人数最多,有9人,所点频率为:$\frac{9}{20}$=0.45,
∴最高矩形的高h=$\frac{0.45}{10}$=0.045.
(Ⅲ)打分在70分以下(不含70分)的同学有6人,其中男生4人,女生2人,
从中抽取3人,基本事件总数n=${C}_{6}^{3}$=20,
有女生被抽中的对立事件是抽中的3名同学都是男生,
∴有女生被抽中的概率p=1-$\frac{m}{n}$=1-$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{4}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
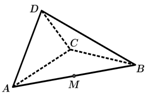 如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.
如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-∞,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com