
| A. | (28,+∞) | B. | [15,+∞) | C. | [28,+∞) | D. | (15,+∞) |
分析 求得x1+1 和x2+1在区间(2,3)内,将原不等式移项,可得$\frac{f({x}_{1}+1)-({x}_{1}+1)-[f({x}_{2}+1)-({x}_{2}+1)]}{({x}_{1}+1)-({x}_{2}+1)}$>0,即有函数y=f(x)-x在(2,3)内递增.求得函数y的导数,可得y′≥0在(2,3)恒成立,即a≥2x2+3x+1在(2,3)内恒成立,求出函数y=2x2+3x+1在[2,3]上的最大值即可.
解答 解:因实数x1,x2在区间(1,2)内,
故x1+1 和x2+1在区间(2,3)内.
不等式$\frac{f({x}_{1}+1)-f({x}_{2}+1)}{{x}_{1}-{x}_{2}}$>1恒成立,
即为$\frac{f({x}_{1}+1)-({x}_{1}+1)-[f({x}_{2}+1)-({x}_{2}+1)]}{({x}_{1}+1)-({x}_{2}+1)}$>0,
即有函数y=f(x)-x在(2,3)内递增.
函数y=f(x)-x=aln(x+1)-x2-x的导数为y′=$\frac{a}{x+1}$-2x-1,
即有y′≥0在(2,3)恒成立.
即a≥(2x+1)(x+1)在(2,3)内恒成立.
由于二次函数y=2x2+3x+1在[2,3]上是单调增函数,
故x=3时,y=2x2+3x+1 在[2,3]上取最大值为28,即有a≥28,
故答案为[28,+∞).
故选:C.
点评 本题考查了导数的应用:判断单调性,考查函数的单调性的运用,考查转化思想,将不等式转化为函数的单调性是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
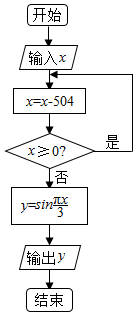
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 43251 | B. | 43512 | C. | 45312 | D. | 45132 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
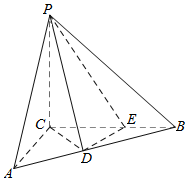 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com