
分析 (1)由正弦定理和正弦函数的性质,即可证明A=2B成立;
(2)由余弦定理和正弦、余弦函数的性质,化简求值即可.
解答 解:(1)证明:△ABC中,a=2bcosB,
由$\frac{a}{sinA}=\frac{b}{sinB}$,得sinA=2sinBcosB=sin2B,
∵0<A,B<π,
∴sinA=sin2B>0,
∴0<2B<π,
∴A=2B或A+2B=π,
若A+2B=π,则B=C,b=c这与“b≠c”矛盾,
∴A+2B≠π;
∴A=2B;
(2)∵a2+c2=b2+2acsinC,
∴$\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=sinC$,
由余弦定理得cosB=sinC,
∵0<B,C<π,
∴$C=\frac{π}{2}-B$或$C=\frac{π}{2}+B$,
①当$C=\frac{π}{2}-B$时,则$A=\frac{π}{2},B=C=\frac{π}{4}$,
这与“b≠c”矛盾,∴$A≠\frac{π}{2}$;
②当$C=\frac{π}{2}+B$时,由(1)得A=2B,
∴$A+B+C=A+2B+\frac{π}{2}=2A+\frac{π}{2}=π$,
∴$A=\frac{π}{4}$.
点评 本题考查了正弦、余弦定理和正弦、余弦函数的应用问题,是基础题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3×{(\frac{5}{6})^{n-1}}-1$ | B. | $3×{(\frac{5}{6})^n}-1$ | C. | $3×{(\frac{5}{6})^{n-1}}+1$ | D. | $3×{(\frac{5}{6})^n}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
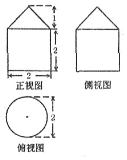
| A. | $\frac{7π}{3}$ | B. | $8+\frac{π}{3}$ | C. | $({4+\sqrt{2}})π$ | D. | $({5+\sqrt{2}})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
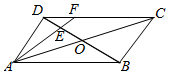 在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )
在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com