
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .记点
.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的动点,且直线
上的动点,且直线![]() 过点
过点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,请求出定点
?若存在,请求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,椭圆;(2)存在,
,椭圆;(2)存在,![]() .
.
【解析】
(1)写出斜率,根据斜率之积为![]() 建立方程,化简即可(2)假设存在的定点
建立方程,化简即可(2)假设存在的定点![]() ,分MN斜率存在或不存在两种情况讨论,设
,分MN斜率存在或不存在两种情况讨论,设![]() ,
,![]() ,当MN斜率存在时,联立方程可求出
,当MN斜率存在时,联立方程可求出![]() ,根据两角相等可得
,根据两角相等可得![]() ,化简即可求出m,验证MN斜率不存在时也成立即可.
,化简即可求出m,验证MN斜率不存在时也成立即可.
(1)由题意得:![]()
![]()
化简得:![]()
![]() 曲线
曲线![]() 的方程为
的方程为![]()
![]() 是中心在坐标原点,焦点在
是中心在坐标原点,焦点在![]() 轴上的椭圆(不含左、右顶点)
轴上的椭圆(不含左、右顶点)
(2)假设存在的定点![]() 符合题意
符合题意
由题意知:直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]()
由题意及(1)知:直线![]() 与直线
与直线![]() 均不重合.
均不重合.
当直线![]() 的斜率
的斜率![]() 存在时
存在时
设其方程为![]() ,
,![]() ,
,![]()
由![]() ,得直线
,得直线![]() 的倾斜角互补,故
的倾斜角互补,故![]()
又![]()
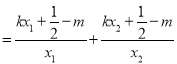
![]()
![]() ①
①
由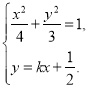 消去
消去![]() ,整理得:
,整理得:![]() .
.
![]()
又![]() ,
,![]() ②
②
代②入①得:![]()
![]() ③
③
![]() 当
当![]() 时,又
时,又![]() 不恒为0
不恒为0
![]() 当且仅当
当且仅当![]() 时,③式成立,即定点
时,③式成立,即定点![]() 满足题意.
满足题意.
当直线![]() 的斜率不存在时,点
的斜率不存在时,点![]() 满足
满足![]() ,也符合题意.
,也符合题意.
综上所述,在 ![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 年俄罗斯索契冬奥会某项目的选拔比赛中,
年俄罗斯索契冬奥会某项目的选拔比赛中,![]() 、
、![]() 两个代表队进行对抗赛,每队三名队员,
两个代表队进行对抗赛,每队三名队员,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,
,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得
,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得![]() 分,负队得
分,负队得![]() 分,设
分,设![]() 队、
队、![]() 队最后所得总分分别为
队最后所得总分分别为![]() 、
、![]() 且
且![]() .
.
对阵队员 |
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 队得分为
队得分为![]() 分的概率;
分的概率;
(2)求![]() 的分布列;并用统计学的知识说明哪个队实力较强.
的分布列;并用统计学的知识说明哪个队实力较强.
查看答案和解析>>
科目:高中数学 来源: 题型:
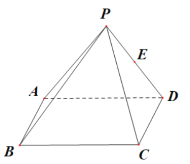
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ,侧面
,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)在棱![]() 上取一点
上取一点![]() 使直线
使直线![]() ∥平面
∥平面![]() 并证明;
并证明;
(2)在(1)的条件下,当棱![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与底面
与底面![]() 所成角为
所成角为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=3上的一动点M在x轴上的投影为N,点P满足![]() .
.
(1)求动点P的轨迹C的方程;
(2)若直线l与圆O相切,且交曲线C于点A,B,试求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且acosC=(2b﹣c)cosA.
(1)若![]() 3,求△ABC的面积;
3,求△ABC的面积;
(2)若∠B<∠C,求2cos2B+cos2C的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com