考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件,利用等比数列的通项公式求出公比,由此能求出数列{an}的通项公式.
(Ⅱ)由已知条件结合(Ⅰ)得到bn=(2n-1)•2n-1,由此利用错位相减法能求出数列{bn}的前n项和Tn.
解答:
解:(Ⅰ)设在等比数列{a
n}中,公比为q,
∵a
1=1,a
1+S
2=a
3,∴2a
1+a
2=a
3,
∴
2a1+a1q=a1q2,
即2+q=q
2,…(2分)
解得q=2或q=-1(舍)…(4分)
所以
an=2n-1…(6分)
(Ⅱ)∵
{}是首项为1,公差为2的等差数列,
∴
=2n-1,
∵
an=2n-1,
∴
bn=(2n-1)•2n-1.…(7分)
∵T
n=b
1+b
2+b
3+…+b
n∴
Tn=1•1+3•2+5•22+…+(2n-1)•2n-1①…(9分)
2Tn=1•2+3•22+5•23+…+(2n-1)•2n②…(10分)
②-①,得
Tn=-1-2•[2+22+…+2n-1]+(2n-1)•2n=-1+4(1-2
n-1)+(2n-1)•2
n=(2n-3)•2
n+3…(12分)
点评:本题考查数列的通项公式和前n项和,是中档题,解题时要注意裂项求和法的合理运用.



 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案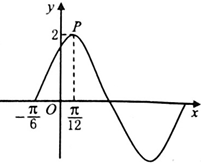 已知函数f(x)=Asin(ωx+φ), (ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ), (ω>0,A>0,φ∈(0,