Question

2．已知函数f（x）=x+2^x，g（x）=x+lnx，$h（x）=x-\sqrt{x}-1$的零点分别为x₁，x₂，x₃，则x₁，x₂，x₃的大小关系是（　　）

• A． x₂＜x₁＜x₃
• B． x₁＜x₂＜x₃
• C． x₁＜x₃＜x₂
• D． x₂＜x₃＜x₁

Answer 1

分析 由函数f（x）=x+2^x，g（x）=x+lnx，$h（x）=x-\sqrt{x}-1$的零点分别为x₁，x₂，x₃，即函数令y₁=2^x，y₂=lnx，y=-$\sqrt{x}$-1与函数y=-x的交点的横坐标分别为x₁，x₂，x₃，作出函数的图象，结合函数的图象可判断

解答 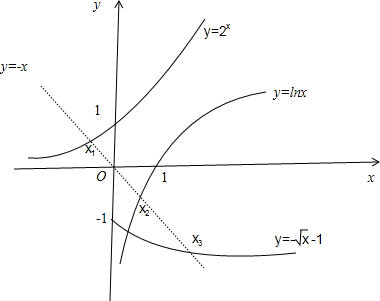解：由函数f（x）=x+2^x，g（x）=x+lnx，$h（x）=x-\sqrt{x}-1$的零点分别为x₁，x₂，x₃，
即函数令y₁=2^x，y₂=lnx，y=-$\sqrt{x}$-1与函数y=-x的交点的横坐标分别为x₁，x₂，x₃，
作出函数的图象，结合图象可得x₁＜x₂＜x₃，
故选：B．

点评 本题主要考查了方程的零点的大小的判断，解题的关键是结合函数的图象，体现了方程与函数的相互转换及数形结合的数学思想的应用．属于难题．