
分析 (1)设动圆圆心的坐标为C(x,y),由题意可得:22+|x|2=(x-2)2+y2,化简整理即可得出.
(2)设P(a,0),A(x1,y1),B(x2,y2).由$\overrightarrow{AM}$=λ$\overrightarrow{MB}$(λ∈R),可知:M,A,B三点共线,设直线AB的方程为:x=my+2,代入抛物线方程可得:y2-4my-8=0..由△PAM与△PBM的面积之比等于$\frac{|PA|}{|PB|}$,可得:PM平分∠APB,因此直线PA,PB的倾斜角互补,即kPA+kPB=0,利用斜率计算公式、根与系数的关系化简即可得出.
解答 解:(1)设动圆圆心的坐标为C(x,y),由题意可得:22+|x|2=(x-2)2+y2,化为:y2=4x.
∴动圆圆心的轨迹方程为:y2=4x.
(2)设P(a,0),A(x1,y1),B(x2,y2).由$\overrightarrow{AM}$=λ$\overrightarrow{MB}$(λ∈R),可知:M,A,B三点共线.
设直线AB的方程为:x=my+2,代入抛物线方程可得:y2-4my-8=0.
∴y1+y2=4m,y1•y2=-8.由△PAM与△PBM的面积之比等于$\frac{|PA|}{|PB|}$,可得:PM平分∠APB,
因此直线PA,PB的倾斜角互补,
∴kPA+kPB=0,∴$\frac{{y}_{1}}{{x}_{1}-a}$+$\frac{{y}_{2}}{{x}_{2}-a}$=0,
把x1=my1+2,x2=my2+2代入可得:$\frac{2m{y}_{1}{y}_{2}+(2-a)({y}_{1}+{y}_{2})}{(m{y}_{1}+2-a)(m{y}_{2}+2-a)}$=0,
∴-16m+(2-a)×4m=0,化为:m(a+2)=0,由于对于任意m都成立,∴a=-2.
故存在定点(-2,0),满足条件.
点评 本题考查了抛物线与圆的标准方程及其性质、直线与抛物线相交问题问题转化为一元二次方程的根与系数的关系、斜率计算公式、角平分线的性质、三角形面积计算公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
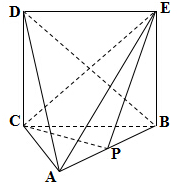 如图所示,△ABC中,AC=1,AB=2,∠ACB=$\frac{π}{2}$,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.
如图所示,△ABC中,AC=1,AB=2,∠ACB=$\frac{π}{2}$,P为AB的中点,且△ABC与正方形BCDE所在平面互相垂直.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,+∞) | B. | (-∞,9) | C. | [3,+∞) | D. | [8,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 4$\sqrt{2}$+2 | C. | 4$\sqrt{2}$-2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com