
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为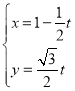 (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() 的直角坐标为
的直角坐标为![]() ,曲线
,曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点F的距离
到焦点F的距离![]() ,倾斜角为α的直线经过焦点F,且与抛物线交于两点A、B。
,倾斜角为α的直线经过焦点F,且与抛物线交于两点A、B。
(1)求抛物线的标准方程及准线方程;
(2)若α为锐角,作线段AB的中垂线m交x轴于点P。证明:![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高一、高二、高三三个年级的青年学生志愿者人数分别为180,120,60,现采用分层抽样的方法从中抽取6名同学去森林公园风景区参加“保护鸟禽,爱我森林”宣传活动.
(1)应从高一、高二、高三三个年级的学生志愿者中分别抽取多少人?
(2)设抽取的6名同学分别用A,B,C,D,E,F表示,现从中随机抽取2名学生承担分发宣传材料的工作设事件M=“抽取的2名学生来自高一年级”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.

完成表格,并判断是否有![]() 以上的把握认为“数学成绩优秀与教学改革有关”;
以上的把握认为“数学成绩优秀与教学改革有关”;

(2)从乙班![]() ,
,![]() ,
,![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在R上是增函数,则下列说法正确的是( )
A.y=-f(x)在R上是减函数
B.y=![]() 在R上是减函数
在R上是减函数
C.y=[f(x)]2在R上是增函数
D.y=af(x)(a为实数)在R上是增函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com