练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知某中学高一、高二、高三三个年级的青年学生志愿者人数分别为180,120,60，现采用分层抽样的方法从中抽取6名同学去森林公园风景区参加“保护鸟禽，爱我森林”宣传活动.

    （1）应从高一、高二、高三三个年级的学生志愿者中分别抽取多少人？

    （2）设抽取的6名同学分别用A，B，C，D，E，F表示，现从中随机抽取2名学生承担分发宣传材料的工作设事件M=“抽取的2名学生来自高一年级”，求事件M发生的概率.

    【答案】（1）从高一、高二、高三三个年级的学生志愿者中分别抽取3人，2人，1人,（2）

    【解析】

    (1)根据分层抽样的方法求解即可.

    (2)利用古典概型的方法枚举所有基本事件求解即可.

    （1）由己知，高一、高二、高三三个年级的学生志愿者人数之比为3：2：1，

    由于采用分层抽样的方法从中抽取6名学生，抽样比为，

    故从高一、高二、高三三个年级的学生志愿者中分别抽取3人，2人，1人.

    （2）从抽取的6名学生中随机抽取2名同学的所有可能结果为，，共15种.

    不妨设抽取的6名学生中，来自高一的是A，B，C，则从抽取的6名学生中随机抽取2名同学来自高一年级的所有可能结果为共3种，

    所以事件M发生的概率为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】据悉,2017年教育机器人全球市场规模已达到8.19亿美元,中国占据全球市场份额10.8%.通过简单随机抽样得到40家中国机器人制造企业,下图是40家企业机器人的产值频率分布直方图.

    （1）求的值；

    （2）在上述抽取的40个企业中任取3个，抽到产值小于500万元的企业不超过两个的概率是多少？

    （3）在上述抽取的40个企业中任取2个,设为产值不超过500万元的企业个数减去超过500万元的企业个数的差值,求的分布列及期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学调查了某班全部名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）


    参加书法社团

    未参加书法社团

    参加演讲社团



    未参加演讲社团



    （1）从该班随机选名同学，求该同学至少参加上述一个社团的概率；

    （2）在既参加书法社团又参加演讲社团的名同学中，有5名男同学名女同学现从这名男同学和名女同学中各随机选人，求被选中且未被选中的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数，若在定义域内存在实数x，满足，则称为“局部奇函数”。为定义在上的“局部奇函数”；q：曲线与x轴交于不同的两点。

    (1)当p为真时，求m的取值范围.

    (2)若“”为真命题，且“”为假命题，求m的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业通过调查问卷（满分50分）的形式对本企业900名员工的工作满意度进行调查，并随机抽取了其中30名员工（其中16名女员工，14名男员工）的得分，如下表：

    女

    47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49

    男

    37 35 34 43 46 36 38 40 39 32 48 33 40 34

    （Ⅰ）现求得这30名员工的平均得分为40.5分，若规定大于平均得分为“满意”，否则为“不满意”，请完成下列表格：

    “满意”的人数

    “不满意”的人数

    合计

    女

    16

    男

    14

    合计

    30

    （Ⅱ）根据上述表中数据，利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下，认为该企业员工“性别”与“工作是否满意”有关？

    参考数据：

    0.10

    0.050

    0.025

    0.010

    0.001

    2.706

    3.841

    5.024

    6.635

    10.828

    参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，直线的参数方程为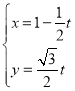（为参数）.以原点为极点，以轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    (Ⅰ）写出直线的普通方程和曲线的直角坐标方程；

    (Ⅱ）若点的直角坐标为，曲线与直线交于两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD为直角梯形，试作出绕其各条边所在的直线旋转所得到的几何体.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，其左顶点在圆上.

    （1）求椭圆的方程；

    （2）若点为椭圆上不同于点 的点，直线与圆的另一个交点为.是否存在点，使得?若存在，求出点的坐标；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）讨论函数的单调性；

    （Ⅱ）当时，在定义域内恒成立，求实数的值.

    查看答案和解析>>

    同步练习册答案