
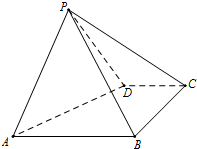
 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.分析 (Ⅰ)由题意取AD的中点G,连接PG、GB、BD,因△PAD是等腰直角三角形,所以PG⊥AD,再由AB=AD,且∠DAB=60°得BG⊥AD,证出AD⊥平面PGB,即AD⊥PB;
(Ⅱ)分别取PA、AB的中点M、N,连结CM、MN、NC,证明四边形ANCD为平行四边形,可得平面CMN∥平面PAD.证明△CBM是直角三角形,可得结论.
解答 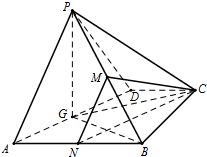 (Ⅰ)证明:取AD的中点G,连接PG、GB、BD∵PA=PD,
(Ⅰ)证明:取AD的中点G,连接PG、GB、BD∵PA=PD,
∴PG⊥AD.(2分)
∵AB=AD,且∠DAB=60°,
∴△ABD是正三角形,∴BG⊥AD,
又∵PG∩BG=G,PG、BG?平面PGB
∴AD⊥平面PGB.
∴AD⊥PB.(5分)
(Ⅱ)解:存在,理由如下:
分别取PA、AB的中点M、N,连结CM、MN、NC,则MN∥PA;
∵ABCD是梯形,且DC平行且等于$\frac{1}{2}$AB,
∴DC平行且等于AN,于是,四边形ANCD为平行四边形,
∴平面CMN∥平面PAD.
由(Ⅰ)知,MN=1,CN=2,在△PBC与在△CBM中:$\frac{PB}{BC}=\frac{BC}{BM}=\sqrt{2}$,
∴△PBC∽△CBM,得CM=$\sqrt{3}$,∴△CBM是直角三角形,
∴${S_{△CMN}}=\frac{1}{2}•CM•MN=\frac{{\sqrt{3}}}{2}$.…(12分)
点评 本题主要考查了线面垂直和平行的判定定理的应用,主要用了中位线和等腰三角形的中线证明线线平行和垂直.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 4+2i | B. | 20+10i | C. | 4-2i | D. | $\frac{20}{3}+\frac{10}{3}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
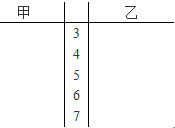 砷是广泛分布于自然界中的非金属元素,长期饮用高砷水会直接危害群众的身心健康和生命安全,而近水农村地区,水质情况更需要关注.为了解甲、乙两地区农村居民饮用水中砷含量的基本情况,分别在两地随机选取10个村子,其砷含量的调查数据如下(单位:mg/1000L):
砷是广泛分布于自然界中的非金属元素,长期饮用高砷水会直接危害群众的身心健康和生命安全,而近水农村地区,水质情况更需要关注.为了解甲、乙两地区农村居民饮用水中砷含量的基本情况,分别在两地随机选取10个村子,其砷含量的调查数据如下(单位:mg/1000L):查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com