
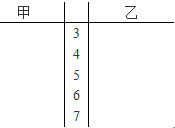
 ���ǹ㷺�ֲ�����Ȼ���еķǽ���Ԫ�أ��������ø���ˮ��ֱ��Σ��Ⱥ�ڵ����Ľ�����������ȫ������ˮũ�������ˮ���������Ҫ��ע��Ϊ�˽�ס���������ũ���������ˮ���麬���Ļ���������ֱ����������ѡȡ10�����ӣ����麬���ĵ����������£���λ��mg/1000L����
���ǹ㷺�ֲ�����Ȼ���еķǽ���Ԫ�أ��������ø���ˮ��ֱ��Σ��Ⱥ�ڵ����Ľ�����������ȫ������ˮũ�������ˮ���������Ҫ��ע��Ϊ�˽�ס���������ũ���������ˮ���麬���Ļ���������ֱ����������ѡȡ10�����ӣ����麬���ĵ����������£���λ��mg/1000L�������� ��I����1����������������ݵ�ƽ����Ϊ$\overline x$���ҵ����������ݵ�ƽ����Ϊ$\overline y$���Ƴ��ҵ���������ˮ���麬�����ߣ�
��2�����þ�Ҷͼ��ֱ���Ƴ�������ҵ���������ˮ���麬�����ߣ�
��II�������֪�����ҵ����漴��ȡһ�����ӣ���Ҫ��פҽ��С��ĸ��ʣ��õ�X�ķֲ��У����������
��� �⣺��I����1��������������ݵ�ƽ����Ϊ$\overline x$��
$\overline x=\frac{1}{10}��52+32+41+72+43+35+45+61+53+44��=47.8$��
���ҵ����������ݵ�ƽ����Ϊ$\overline y$��$\overline y=\frac{1}{10}��44+56+38+61+72+57+64+71+58+62��=58.3$��
�����ϼ������ɵ�$\overline{x}��\overline{y}$����˿��Կ����ҵ���������ˮ���麬�����ߣ�
��2���Ӿ�Ҷͼ���Կ����������ĵ���������80%��Ҷ�����ھ���3����4����5�������ҵ�����80%��Ҷ�����ھ���5����6����7��������ҵ���������ˮ���麬�����ߡ���5�֣�
��II�������֪�����ҵ����漴��ȡһ�����ӣ���Ҫ��פҽ��С��ĸ��ʣ�
$\begin{array}{l}P��X=0��=C_3^0•{��\frac{4}{5}��^0}•{��\frac{1}{5}��^3}=\frac{1}{125}��P��X=1��=C_3^1•{��\frac{4}{5}��^1}•{��\frac{1}{5}��^2}=\frac{12}{125}\\ P��X=2��=C_3^2•{��\frac{4}{5}��^2}•{��\frac{1}{5}��^1}=\frac{48}{125}��P��X=3��=C_3^3•{��\frac{4}{5}��^3}•{��\frac{1}{5}��^0}=\frac{64}{125}\end{array}$
X�ķֲ���Ϊ����10�֣�
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{125}$ | $\frac{12}{125}$ | $\frac{48}{125}$ | $\frac{64}{125}$ |
���� ���⿼�龥Ҷͼ�Լ���ɢ����������ķֲ������������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
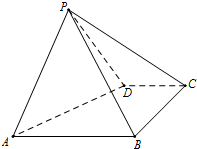 ��ͼ������P-ABCD�У�����ABCD��ֱ�����Σ�AB��CD����DAB=60�㣬AB=AD=2CD=2������PAD�͵���ABCD���ҡ�PAD����ADΪ�ĵ��������Σ�
��ͼ������P-ABCD�У�����ABCD��ֱ�����Σ�AB��CD����DAB=60�㣬AB=AD=2CD=2������PAD�͵���ABCD���ҡ�PAD����ADΪ�ĵ��������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x-3y-9=0 | B�� | 3x-2y-11=0 | C�� | 3x+2y-7=0 | D�� | x-y-5=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y2-$\frac{{x}^{2}}{3}$=1 | B�� | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C�� | $\frac{{x}^{2}}{3}$-y2=1 | D�� | x2-$\frac{{y}^{2}}{3}$=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 607 | B�� | 328 | C�� | 253 | D�� | 007 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���Vp���ţ��Vp�� | B�� | �V�����Vp���ģ��Vp���� | C�� | ���Vp���ģ��Vp�� | D�� | �V��p��p�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.5 | B�� | 1.5 | C�� | 2.5 | D�� | 3.5 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com