练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．由观测的样本数据算得变量x与y满足线性回归方程$\widehaty=0.6x-0.5$，已知样本平均数$\overline x=5$，则样本平均数$\overline y$的值为（　　）
    A．0.5B．1.5C．2.5D．3.5

    分析 直接利用回归直线方程经过样本中心，求解即可．

    解答 解：线性回归方程$\widehaty=0.6x-0.5$，已知样本平均数$\overline x=5$，则样本平均数$\overline y$=0.6×5-0.5=2.5．
    故选：C．

    点评 本题考查回归直线方程的应用，基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

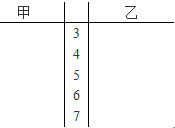    9．砷是广泛分布于自然界中的非金属元素，长期饮用高砷水会直接危害群众的身心健康和生命安全，而近水农村地区，水质情况更需要关注．为了解甲、乙两地区农村居民饮用水中砷含量的基本情况，分别在两地随机选取10个村子，其砷含量的调查数据如下（单位：mg/1000L）：
    甲地区的10个村子饮用水中砷的含量：
    52   32   41   72   43   35   45   61   53   44
    乙地区的10个村子饮用水中砷的含量：
    44   56   38   61   72   57   64   71   58   62
    （Ⅰ）根据两组数据完成茎叶图，试比较两个地区中哪个地区的饮用水中砷含量更高，并说明理由；
    （Ⅱ）国家规定居民饮用水中砷的含量不得超过50，现医疗卫生组织决定向两个地区中每个砷超标的村子派驻一个医疗救助小组．用样本估计总体，把频率作为概率，若从乙地区随机抽取3个村子，用X表示派驻的医疗小组数，试写出X的分布列并求X的期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}，x≤0}\\{1-3x，x＞0}\end{array}\right.$，若f（2a2-3）＞f（5a），则实数a的取值范围是（-$\frac{1}{2}$，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知椭圆以坐标原点为中心，坐标轴为对称轴，以抛物线y2=16x的焦点为其中一个焦点，以双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的焦点为顶点．
    （1）求椭圆的标准方程；
    （2）已知点A（-1，0），B（1，0），且C，D分别为椭圆的上顶点和右顶点，点M是线段CD上的动点，求$\overrightarrow{AM}$•$\overrightarrow{BM}$的最小值；
    （3）若E，F是椭圆上关于原点对称的两点，P是椭圆上任意一点，则当直线PE，PF的斜率都存在，并记为kPE，kPF时，kPE•kPF是否为定值，若时求出这个定值，若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．数列{an}中，若Sn=n2an，a1=$\frac{1}{2}$，则an=$\frac{1}{n（n+1）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设函数f（x）=cos（$\frac{π}{2}$-x）cosx-sin2（π-x）-$\frac{1}{2}$．
    （Ⅰ） 求函数f（x）的最小正周期和单调递增区间；
    （Ⅱ） 若f（α）=$\frac{3\sqrt{2}}{10}$-1，且α∈（$\frac{π}{8}$，$\frac{3π}{8}$），求f（α-$\frac{π}{8}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

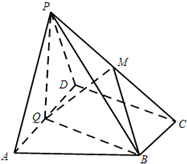    8．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，$BC=\frac{1}{2}AD=1$，$CD=\sqrt{3}$．
    （1）求证：平面MQB⊥平面PAD；
    （2）若满足BM⊥PC，求异面直线AP与BM所成角的余弦值；
    （3）若二面角M-BQ-C大小为30°，求QM的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=xlnx．
    （Ⅰ）讨论函数f（x）的单调性；
    （Ⅱ）对于任意正实数x，不等式f（x）＞kx-$\frac{1}{2}$恒成立，求实数k的取值范围；
    （Ⅲ）求证：当a＞3时，对于任意正实数x，不等式f（a+x）＜f（a）•ex恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．设M是△ABC的重心，若A=$\frac{π}{3}$，$\overrightarrow{AB}•\overrightarrow{AC}=3$，则$|\overrightarrow{AM}|$的最小值为$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案