
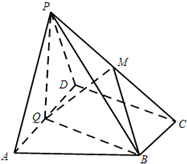
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.分析 (1)证明QB⊥AD,根据平面PAD⊥平面ABCD可得BQ⊥平面PAD,即可证明平面MQB⊥平面PAD;
(2)确定PQ⊥平面ABCD,建立空间直角坐标系,求出$\overrightarrow{AP}=(-1,0,\sqrt{3}),\overrightarrow{BM}=(-\frac{6}{7},-\frac{{\sqrt{3}}}{7},\frac{{\sqrt{3}}}{7})$,利用向量的夹角公式求异面直线AP与BM所成角的余弦值;
(3)根据二面角M-BQ-C大小为30°,利用向量的夹角公式,即可求QM的长.
解答  (1)证明:∵AD∥BC,BC=$\frac{1}{2}$AD,Q为AD的中点,
(1)证明:∵AD∥BC,BC=$\frac{1}{2}$AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,
∴CD∥BQ. …(1分)
∵∠ADC=90°∴∠AQB=90°,即QB⊥AD.
又∵平面PAD⊥平面ABCD且平面PAD∩平面ABCD=AD,…(2分)
∴BQ⊥平面PAD. …(3分)
∵BQ?平面MQB,
∴平面MQB⊥平面PAD. …(4分)
(2)解:∵PA=PD,Q为AD的中点,
∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD. …(5分)
如图,以Q为原点建立空间直角坐标系.则Q(0,0,0),A(1,0,0),$P(0,0,\sqrt{3})$,$B(0,\sqrt{3},0)$,$C(-1,\sqrt{3},0)$
由 $\overrightarrow{PM}=λ\overrightarrow{PC}=λ(-1,\sqrt{3},-\sqrt{3})$,且0≤λ≤1,得$M(-λ,\sqrt{3}λ,\sqrt{3}-\sqrt{3}λ)$
∵BM⊥PC,
∴$\overrightarrow{BM}•\overrightarrow{PC}=(-λ,\sqrt{3}λ-\sqrt{3},\sqrt{3}-\sqrt{3}λ)•(-1,\sqrt{3},-\sqrt{3})=7λ-6=0$…(6分)
∴$\overrightarrow{AP}=(-1,0,\sqrt{3}),\overrightarrow{BM}=(-\frac{6}{7},-\frac{{\sqrt{3}}}{7},\frac{{\sqrt{3}}}{7})$
设异面直线AP与BM所成角为θ,则cosθ=$|cos<\overrightarrow{AP},\overrightarrow{BM}>|=|\frac{{\overrightarrow{AP}•\overrightarrow{BM}}}{{|\overrightarrow{AP}||\overrightarrow{BM}|}}|$=$\frac{9}{84}\sqrt{42}$…(9分)
∴异面直线AP与BM所成角的余弦值为$\frac{9}{84}\sqrt{42}$…(10分),
(3)解:由(2)知平面BQC的法向量为$\overrightarrow n=(0,0,1)$…(11分)
由 $\overrightarrow{QM}=λ\overrightarrow{QP}+(1-λ)\overrightarrow{QC}$,且0≤λ≤1,得$\overrightarrow{QM}=(λ-1,\sqrt{3}(1-λ),\sqrt{3}λ)$
又$\overrightarrow{QB}=(0,\sqrt{3},0)$,
∴平面MBQ法向量为$\overrightarrow m=(\sqrt{3},0,\frac{1-λ}{λ})$. …(13分)
∵二面角M-BQ-C为30°,∴$cos{30°}=|\frac{\overrightarrow n•\overrightarrow m}{{|{\overrightarrow n}||{\overrightarrow m}|}}|=\frac{{\sqrt{3}}}{2}$,
∴$λ=\frac{1}{2}$.∴|QM|=$\frac{{\sqrt{7}}}{2}$…(15分)
点评 本题考查平面与平面垂直,考查异面直线AP与BM所成角的余弦值,考查二面角大小的确定,考查向量知识的运用,综合性强.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬p) | B. | ¬((¬p)∧(¬p)) | C. | (¬p)∧(¬p) | D. | ¬(p∨p) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.5 | B. | 1.5 | C. | 2.5 | D. | 3.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
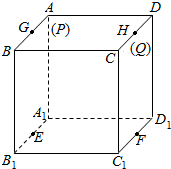 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )| A. | 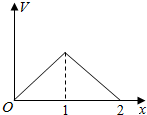 | B. | 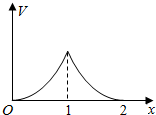 | ||
| C. | 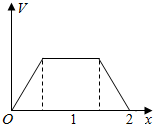 | D. | 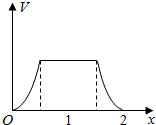 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com