练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．甲乙两位同学最近五次模考数学成绩茎叶图如图，则平均分数较高和成绩比较稳定的分别是（　　）
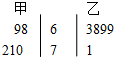
    A．甲、甲B．乙、甲C．甲、乙D．乙、乙

    分析 分别求出甲、乙两位同学某学科的连续五次考试成绩的平均数和方差，由此能求出结果

    解答 解：$\overline{{x}_{甲}}$=$\frac{1}{5}$（68+69+70+71+72）=70，
    S甲2=$\frac{1}{5}$[（68-70）2+（69-70）2+（70-70）2+（71-70）2+（72-70）2]=2，
    $\overline{{x}_{乙}}$=$\frac{1}{5}$（63+68+69+69+71）=68，
    S乙2=$\frac{1}{5}$[（63-68）2+（68-68）2+（69-68）2+（68-69）2+（71-68）2]=4，
    ∴平均分数较高的是甲，成绩较为稳定的是甲．
    故选A．

    点评 本题考查平均数和方差的求法，是基础题，解题时要认真审题，注意茎叶图的合理运用

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

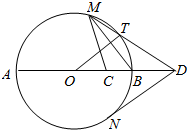    6．如图，AB是圆O的直径，C是半径OB的中点，D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M、T（不与A、B重合），DN与圆O相切于点N，连结MC，MB，OT．
    （Ⅰ）求证：DT•DM=DO•DC；
    （Ⅱ）若∠DOT=30°，求∠BMC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知椭圆以坐标原点为中心，坐标轴为对称轴，以抛物线y2=16x的焦点为其中一个焦点，以双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的焦点为顶点．
    （1）求椭圆的标准方程；
    （2）已知点A（-1，0），B（1，0），且C，D分别为椭圆的上顶点和右顶点，点M是线段CD上的动点，求$\overrightarrow{AM}$•$\overrightarrow{BM}$的最小值；
    （3）若E，F是椭圆上关于原点对称的两点，P是椭圆上任意一点，则当直线PE，PF的斜率都存在，并记为kPE，kPF时，kPE•kPF是否为定值，若时求出这个定值，若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设函数f（x）=cos（$\frac{π}{2}$-x）cosx-sin2（π-x）-$\frac{1}{2}$．
    （Ⅰ） 求函数f（x）的最小正周期和单调递增区间；
    （Ⅱ） 若f（α）=$\frac{3\sqrt{2}}{10}$-1，且α∈（$\frac{π}{8}$，$\frac{3π}{8}$），求f（α-$\frac{π}{8}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

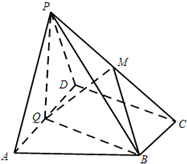    8．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，$BC=\frac{1}{2}AD=1$，$CD=\sqrt{3}$．
    （1）求证：平面MQB⊥平面PAD；
    （2）若满足BM⊥PC，求异面直线AP与BM所成角的余弦值；
    （3）若二面角M-BQ-C大小为30°，求QM的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数$f（x）=-aln\frac{1}{x}-b{x^2}$图象上一点P（2，f（2））处的切线方程为y=-3x+2ln2+2．．
    （1）求a，b的值；
    （2）若方程f（x）+m=0在$[\frac{1}{e}，e]$内有两个不等实根，求m的取值范围（其中e为自然对数的底，e≈2.7）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=xlnx．
    （Ⅰ）讨论函数f（x）的单调性；
    （Ⅱ）对于任意正实数x，不等式f（x）＞kx-$\frac{1}{2}$恒成立，求实数k的取值范围；
    （Ⅲ）求证：当a＞3时，对于任意正实数x，不等式f（a+x）＜f（a）•ex恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．PM2.5是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物）．为了探究车流量与PM2.5的浓度是否相关，现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如下表：
    时间周一周二周三周四周五
    车流量x（万辆）5051545758
    PM2.5的浓度y（微克/立方米）6970747879
    （Ⅰ）根据上表数据，用最小二乘法求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$；
    （Ⅱ）若周六同一时间段车流量是25万辆，试根据（Ⅰ）求出的线性回归方程预测，此时PM2.5的浓度为多少（保留整数）？
    （参考公式：$\hat b=\frac{{\sum_{i=1}^5{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^5{{{（{x_i}-\overline x）}^2}}}}，\overline y=\hat b•\overline x+\hat a$，参考数据：$\sum_{i=1}^5{x_i}=270，\sum_{i=1}^5{y_i}=370$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知正数a，b，c满足a2+b2+c2=6．
    （Ⅰ）求a+2b+c的最大值M；
    （Ⅱ）在（Ⅰ）的条件下，若不等式|x+1|+|x+m|≥M恒成立，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案