
���� ��1��ͨ�������ߡ�˫���߷��̣����ø��ԵĶ�����㼴�ɣ�
��2��ͨ����M��x0��y0������ֱ֪��CD�ķ��̣����ö��κ��������ʼ���$\overrightarrow{AM}$•$\overrightarrow{BM}$����Сֵ��
��3��ͨ�����E��m��n���ɵ�F��-m��-n������P��x��y��������б�ʵĹ�ʽ���㼴�ɣ�
��� �⣺��1��������y2=16x�Ľ��㣨4��0����
˫����$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1�Ľ��㣨��5��0����
����Բ�ı�����Ϊ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����
��a=5��c=4����b2=25-16=9��
����Բ�ı�����Ϊ��$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$��
��2����M��x0��y0����������ֱ֪��CD�ķ���Ϊ$\frac{x}{5}+\frac{y}{3}=1$��
��y=-$\frac{3}{5}$x+3��0��x��5����
��y0=-$\frac{3}{5}$x0+3��0��x0��5����$\overrightarrow{AM}$=��x0+1��y0����$\overrightarrow{BM}$=��x0-1��y0����
��$\overrightarrow{AM}$•$\overrightarrow{BM}$=x02+y02-1
=x02+��-$\frac{3}{5}$x0+3��2-1
=$\frac{34}{25}$��x0-$\frac{45}{34}$��2+$\frac{191}{34}$��0��x0��5����
�൱x0=$\frac{45}{34}$ʱ��$\overrightarrow{AM}$•$\overrightarrow{BM}$ȡ����СֵΪ$\frac{191}{34}$��
��3�����ۣ�kPE•kPF�Ƕ�ֵ���Ҷ�ֵΪ-$\frac{9}{25}$��
�������£�
���E��������m��n�������F��������-m��-n����$\frac{{m}^{2}}{25}+\frac{{n}^{2}}{9}=1$��
�����P��������x��y������$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$��
��kPE=$\frac{y-n}{x-m}$��kPF=$\frac{y+n}{x+m}$���ã�kPE•kPF=$\frac{y-n}{x-m}$•$\frac{y+n}{x+m}$=$\frac{{y}^{2}-{n}^{2}}{{x}^{2}-{m}^{2}}$��
����ã�kPE•kPF=$\frac{\frac{9}{25}��{m}^{2}-{x}^{2}��}{{x}^{2}-{m}^{2}}$=-$\frac{9}{25}$��
���� ������һ��ֱ����Բ���ߵ��ۺ��⣬���������������������������⡢��������������ע����ⷽ���Ļ��ۣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x-3y-9=0 | B�� | 3x-2y-11=0 | C�� | 3x+2y-7=0 | D�� | x-y-5=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��-7} | B�� | {x|-7��x��1} | C�� | {x|x��1} | D�� | {x|x��-7��x��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.5 | B�� | 1.5 | C�� | 2.5 | D�� | 3.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
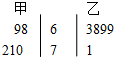
| A�� | �ס��� | B�� | �ҡ��� | C�� | �ס��� | D�� | �ҡ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com