
分析 (Ⅰ)分析题目已知a2+b2+c2=6,求a+2b+c的最大值,考虑到柯西不等式(a2+b2+c2)(12+22+12)≥(a+2b+c)2,即可得到答案.
(Ⅱ)利用绝对值不等式的几何意义可求得|x+1|+|x+m|≥|x+1-(x+m)|=|m-1|,由题意及(Ⅰ)得,|m-1|≥6,从而可求得实数m的取值范围.
解答 解:(Ⅰ)因为已知a、b、c是实数,且a2+b2+c2=6,
根据柯西不等式有(a2+b2+c2)(12+22+12)≥(a+2b+c)2
故(a+2b+c)2≤36,即a+2b+c≤6
即a+2b+c的最大值为6,
当且仅当$\frac{a}{1}=\frac{b}{2}=\frac{c}{1}$,即当a=c=1,b=2时取得最大值.…(4分)
(Ⅱ)因为|x+1|+|x+m|≥|x+1-(x+m)|=|m-1|,
由题意及(Ⅰ)得,|m-1|≥6,得m≥7或m≤-5.
综上,实数m的取值范围为m≥7或m≤-5.…(7分)
点评 本题考查柯西不等式,考查绝对值不等式的解法,掌握绝对值不等式的几何意义是解决问题的关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
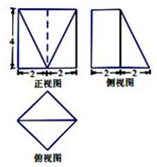 若一个几何体的三视图如图所示,则该几何体的体积是( )
若一个几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | $\frac{80}{3}$ | D. | $\frac{160}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
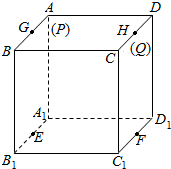 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )| A. | 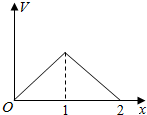 | B. | 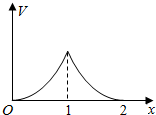 | ||
| C. | 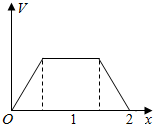 | D. | 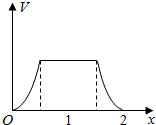 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$),k∈Z | B. | (kπ+$\frac{π}{8}$,kπ+$\frac{3π}{8}$),k∈Z | ||
| C. | (kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$),k∈Z | D. | (kπ+$\frac{3π}{8}$,kπ+$\frac{5π}{8}$),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -3 | C. | -$\frac{5}{2}$ | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com