
| A. | $\frac{3}{2}$ | B. | -3 | C. | -$\frac{5}{2}$ | D. | 5 |
分析 利用DP⊥AB可知,$\overrightarrow{DP}•\overrightarrow{AB}=0$,再利用向量加法和减法的三角形法则以及平行四边形法则,将$\overrightarrow{OP}$•$\overrightarrow{AB}$用$\overrightarrow{OA}$,$\overrightarrow{OB}$和$\overrightarrow{DP}$表示,即可求得答案.
解答 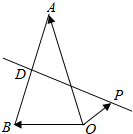 解:设线段AB的垂直平分线与AB的交点为D,则D为AB的中点,
解:设线段AB的垂直平分线与AB的交点为D,则D为AB的中点,
根据向量加法的平行四边形法则,则有$\overrightarrow{OD}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$,
∵DP⊥AB,
∴$\overrightarrow{DP}•\overrightarrow{AB}=0$,
∴$\overrightarrow{OP}$•$\overrightarrow{AB}$=$\overrightarrow{OP}•(\overrightarrow{OB}-\overrightarrow{OA})$=($\overrightarrow{OD}+\overrightarrow{DP}$)•($\overrightarrow{OB}-\overrightarrow{OA}$)
=[$\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$+$\overrightarrow{DP}$]•($\overrightarrow{OB}-\overrightarrow{OA}$)
=$\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})•(\overrightarrow{OB}-\overrightarrow{OA})$$+\overrightarrow{DP}•\overrightarrow{AB}$
=$\frac{1}{2}(|\overrightarrow{OB}{|}^{2}-|\overrightarrow{OA}{|}^{2})$
=$\frac{1}{2}(4-9)=-\frac{5}{2}$.
故选:C.
点评 本题考查了平面向量数量积的运算,解决平面向量数量积的问题,一般有三种方法:向量转化法,坐标化法,特殊值法.运用转化法求解的关键是运用向量加法和减法的三角形法则或平行四边形法则,将要求的向量一步一步向已知的向量转化.属于中档题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 推销员编号 | 1 | 2 | 3 | 4 |
| 工作年限x/(年) | 3 | 5 | 10 | 14 |
| 年推销金额y/(万元) | 2 | 3 | 7 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 671 | B. | 672 | C. | 1342 | D. | 1344 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com