
分析 由A=$\frac{π}{3}$,$\overrightarrow{AB}•\overrightarrow{AC}=3$,可求得|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=6,由点M是△ABC的重心,得$\overrightarrow{AM}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$,两边平方后利用不等式求得最值.
解答 解:∵A=$\frac{π}{3}$,$\overrightarrow{AB}•\overrightarrow{AC}=3$,
∴|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos$\frac{π}{3}$=3,即|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=6,
由点M是△ABC的重心,∴$\overrightarrow{AM}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$,
∴$|\overrightarrow{AM}{|}^{2}=\frac{1}{9}(|\overrightarrow{AB}{|}^{2}+2\overrightarrow{AB}•\overrightarrow{AC}+|\overrightarrow{AC}{|}^{2})$=$\frac{1}{9}(|\overrightarrow{AB}{|}^{2}+|\overrightarrow{AC}{|}^{2}+6)$
$≥\frac{1}{9}(2|\overrightarrow{AB}|•|\overrightarrow{AC}|+6)$=$\frac{1}{9}$(2×6+6)=2,
∴|$\overrightarrow{AM}$|≥$\sqrt{2}$,当且仅当|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|=$\sqrt{6}$时取等号,
∴|$\overrightarrow{AM}$|的最小值为$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查平面向量数量积的运算、不等式求最值,注意不等式求最值时适用的条件,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0.5 | B. | 1.5 | C. | 2.5 | D. | 3.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
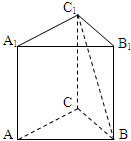 如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.
如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
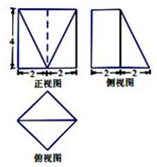 若一个几何体的三视图如图所示,则该几何体的体积是( )
若一个几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | $\frac{80}{3}$ | D. | $\frac{160}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
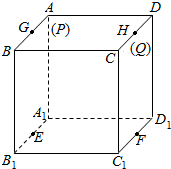 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )| A. | 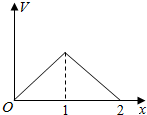 | B. | 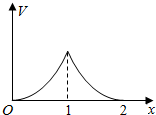 | ||
| C. | 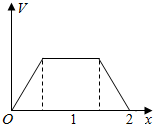 | D. | 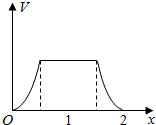 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
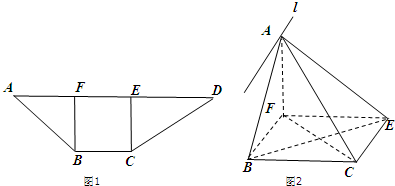
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com