
分析 (Ⅰ)计算按钮第一次、第二次按下后均出现蓝色背景与第一次、第二次按下后依次出现绿色、蓝色背景的概率,再求和即可;
(Ⅱ)考虑第n-1次按下按钮后出现蓝色背景的概率与出现绿色背景的概率,计算第n-1次、第n次按下按钮后均出现蓝色背景与第n-1次、第n次按下按钮后依次出现绿色背景、蓝色背景的概率,求和得Pn与Pn-1的递推式;
(Ⅲ)由得Pn与Pn-1的递推式,得出$\{{P_n}-\frac{9}{19}\}$是等比数列,求出Pn的通项公式即可.
解答 解:(Ⅰ)若按钮第一次、第二次按下后均出现蓝色背景,
则其概率为$\frac{1}{2}×\frac{1}{3}=\frac{1}{6}$;
若按钮第一次、第二次按下后依次出现绿色背景、蓝色背景,
则其概率为$\frac{1}{2}×\frac{3}{5}=\frac{3}{10}$;
所以,所求的概率为${P_2}=\frac{1}{6}+\frac{3}{10}=\frac{7}{15}$;…(4分)
(Ⅱ)第n-1次按下按钮后出现蓝色背景的概率为Pn-1(n∈N,n≥2),
则出现绿色背景的概率为1-Pn-1;
若第n-1次、第n次按下按钮后均出现蓝色背景,
则其概率为${P_{n-1}}×\frac{1}{3}$;
若第n-1次、第n次按下按钮后依次出现绿色背景、蓝色背景,
则其概率为$(1-{P_{n-1}})×\frac{3}{5}$;
所以,${P_n}=\frac{1}{3}{P_{n-1}}+\frac{3}{5}(1-{P_{n-1}})=-\frac{4}{15}{P_{n-1}}+\frac{3}{5}$,
(其中n∈N,n≥2);…(8分)
(Ⅲ)由(2)得,${P_n}-\frac{9}{19}=-\frac{4}{15}({P_{n-1}}-\frac{9}{19})$,
即$\frac{{P}_{n}-\frac{9}{19}}{{P}_{n-1}-\frac{9}{19}}$=-$\frac{4}{15}$,(其中n∈N,n≥2);
所以,$\{{P_n}-\frac{9}{19}\}$是首项为$\frac{1}{38}$,公比为$-\frac{4}{15}$的等比数列,
所以,Pn-$\frac{9}{19}$=$\frac{1}{38}$•${(-\frac{4}{15})}^{n-1}$;
即${P_n}=\frac{1}{38}{(-\frac{4}{15})^{n-1}}+\frac{9}{19}(n∈N,n≥1)$.…(12分)
点评 本题考查了古典概型的概率的应用问题,也考查了递推数列的应用问题,考查了等比数列的定义与通项公式的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
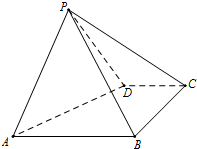 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
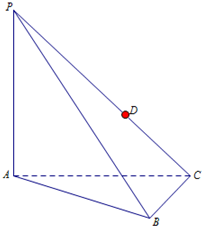 如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.
如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com