
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 先找出全称命题,然后再根据各自的性质判断真假.①素数又叫做质数,质数与合数是根据一个数因数的故数的多少来进行分类,奇数与偶数是根据是不是2的倍数来进行分类的;最小的素数(质数)是2,2是偶数;由此解答.②③均由概念或者公理判定.
解答 解:对于①最小的素数(质数)是2,2是偶数不是奇数,因此所有的素数都是奇数,这种说法是错误的.故①不满足条件
对于②因?x∈R,(x-1)2≥0,所以(x-1)2+1≥1,所以②为真命题.由全称命题和特称命题的定义知②是全称命题.故②满足条件.
对于③有的无理数的平方还是无理数该命题时真命题,但是存在性命题.故③不满足条件
故选:B
点评 本题主要考查全称命题和特称命题的概念及素数、无理数的概念是解答该题的关键,属于基础题型.


科目:高中数学 来源: 题型:解答题
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1或3 | B. | 3 | C. | 27 | D. | -1或27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线m,n和平面α成等角 | B. | m⊥α且n⊥α | ||
| C. | m∥α且n?α | D. | m∥α且n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
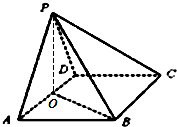 如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com