
分析 (1)先求出函数f(x)的定义域,当a=1是求出f(x)的导数,得到极值点,写出单调区间即可.
(2)表示出f(x)在x=x0处的切线,构造新的函数g(x),则由题意知g(x)≤0恒成立,求解即可.
解答 解:(1)定义域为{x|x≠0,x∈R},当x>0⇒$f'(x)=\frac{1}{x}-2x+1$;当x<0⇒
$f'(x)=\frac{1}{x}-2x+1$.故$f'(x)=\frac{1}{x}-2x+1=-\frac{2{x}^{2}-x-1}{x}=0$⇒${x}_{1}=-\frac{1}{2},{x}_{2}=1$,
从而f(x)的单调递增区间为$(-∞,-\frac{1}{2}),(0,1)$.
(2)$f'(x)=\frac{-2{x}^{2}+ax+1}{x}$,l:y=f'(x0)(x-x0)+f(x0)
令g(x)=f(x)-f'(x0)(x-x0)-f(x0),由题意,g(x)≤0恒成立.
g'(x)=f'(x)-f'(x0)=-$\frac{2(x-{x}_{0})(x+\frac{1}{2{x}_{0}})}{x}$
x0>0时:若x>0,则g(x)max=g(x0),若x<0,则$g(x)_{max}=g(-\frac{1}{2{x}_{0}})$
x0<0时:若x>0,则$g(x)_{max}=g(-\frac{1}{2{x}_{0}})$,若x<0,则g(x)max=g(x0)
综上,原条件等价于g(x0)≤0且$g(-\frac{1}{2{x}_{0}})≤0$,易得g(x0)=0符合题意.
故$g(-\frac{1}{2{x}_{0}})≤0$⇒$ln(2{x}_{0}^{2})+{x}_{0}^{2}-\frac{1}{4{x}_{0}^{2}}≥0$.令t=${x}_{0}^{2}$⇒$ln(2t)+t-\frac{1}{4t}≥0$
设h(t)=ln(2t)+t-$\frac{1}{4t}$⇒$h'(t)=\frac{(2t+1)^{2}}{4{t}^{2}}>0$⇒h(t)↑,又$h(\frac{1}{2})=0$
∴$h(t)≥0=g(\frac{1}{2})$?$t≥\frac{1}{2}$⇒${\;}x_{0}∈(-∞,-\frac{\sqrt{2}}{2}]∪[\frac{\sqrt{2}}{2},+∞)$
点评 本题主要考查利用导数求函数的单调区间以及利用导数证明函数小于零或者大于零的问题,属于难题,在高考中作压轴题出现.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{84}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1 | ||
| C. | $\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1或$\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
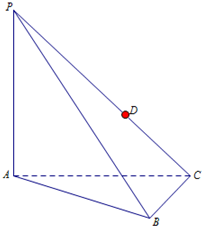 如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.
如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
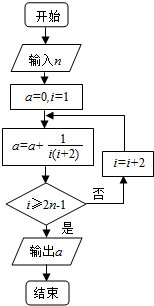
| A. | $\frac{2015}{4031}$ | B. | $\frac{4030}{4031}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{2015}{4029}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com