
分析 (Ⅰ)(i)设圆方程为x2+y2+Dx+Ey+F=0,利用待定系数法求圆C的方程;
(ii)求出以PR为直径的圆的圆心S到CD的距离,证明d=r,即可得出结论;
(Ⅱ)点N在圆E:x2+(y+1)2=4上,又点N在圆C上,圆E与圆C有公共点,进而确定不等式关系求得a的范围.
解答 解:(Ⅰ)设圆方程为x2+y2+Dx+Ey+F=0,则圆心为$(-\frac{D}{2},-\frac{E}{2})$.…(1分)
(i)由题意知$\left\{{\begin{array}{l}{-\frac{E}{2}=-\frac{D}{2}-2}\\{13+3D-2E+F=0}\\ \begin{array}{l}\\ 25-5E+F=0\end{array}\end{array}}\right.$…(2分)
解得:D=0,E=4,F=-5∴圆C:x2+(y+2)2=9…(3分)
(ii)知P(0,1)、B(0,-5),则l:y=1
设D(m,n)(m≠0)$DB:\;y=\frac{n+5}{m}x-5$,$R(\frac{6m}{n+5},\;1)$
以PR为直径的圆的圆心$S(\frac{3m}{n+5},\;1)$,半径$r=\frac{3|m|}{|n+5|}$ ….(5分)
$CD:y=\frac{n+2}{m}x-2$即(n+2)x-my-2m=0…(6分)
以PR为直径的圆的圆心S到CD的距离设为d
则$d=\frac{{|{\frac{3m(n+2)}{n+5}-3m}|}}{{\sqrt{{{(n+2)}^2}+{m^2}}}}=\frac{9|m|}{{|n+5|\sqrt{{{(n+2)}^2}+{m^2}}}}$.…(7分)
又点D在圆C上,∴m2+(n+2)2=9,
∴$d=\frac{3|m|}{|n+5|}=r$
故以PR为直径的圆与直线CD总相切 …(8分)
(Ⅱ)设圆心C(a,a-2),设N(x,y),则
∵|MN|=2|NO|,
∴x2+(y-3)2=4x2+4y2,
∴点N在圆E:x2+(y+1)2=4上 …(10分)
又点N在圆C上,
∴圆E与圆C有公共点,
∴$3-2≤|EC|=\sqrt{2{a^2}-2a+1}≤3+2$…(11分)
∴-3≤a≤0或1≤a≤4….(12分)
点评 本题主要考查了直线与圆的方程的应用.考查了学生的分析推理和基本的运算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
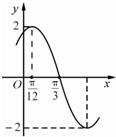 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
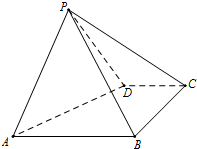 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x-3y-9=0 | B. | 3x-2y-11=0 | C. | 3x+2y-7=0 | D. | x-y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com