
分析 (Ⅰ)$f(x)={x^2}-5|x-a|+2a=\left\{{\begin{array}{l}{{x^2}-5x+7a,(x≥a)}\\{{x^2}+5x-3a,(x≤a)}\end{array}}\right.$,结合0<a<3,x∈[a,3],对a的取值进行分类讨论,结合二次函数的单调性,可得f(x)的单调区间;
(Ⅱ)不妨设x1≤a≤x2,对a的取值进行分类讨论,分别构造出|x1-x2|的最大值为h(k)的表达式,分析其单调性后,可得h(k)的取值范围.
解答 解:(Ⅰ)$f(x)={x^2}-5|x-a|+2a=\left\{{\begin{array}{l}{{x^2}-5x+7a,(x≥a)}\\{{x^2}+5x-3a,(x≤a)}\end{array}}\right.$
因为x∈[a,3],f(x)=x2-5x+7a
若$0<a<\frac{5}{2}$,则f(x)在$[a,\frac{5}{2}]$上为减函数,在$[\frac{5}{2},3]$上为增函数;
若$a≥\frac{5}{2}$,则f(x)=x2+5x-3a在x∈[a,3]上为增函数
(Ⅱ)因为x1,x2满足(x1-a)(x2-a)≤0,不妨设x1≤a≤x2
①当$a≥\frac{5}{2}$时,k≥f(a)=a2+2a,
${x_1}=\frac{{-5-\sqrt{25+4k+12a}}}{2},{x_2}=\frac{{5+\sqrt{25+4k-28a}}}{2}$
$\begin{array}{l}∴|{x_1}-{x_2}{|_{max}}={x_2}-{x_1}=\frac{{5+\sqrt{25+4k-28a}}}{2}-\frac{{-5-\sqrt{25+4k+12a}}}{2}\\=5+\frac{1}{2}[\sqrt{25+4k-28a}+\sqrt{25+4k+12a}]=h(k)\end{array}$
因为h(k)关于k为增函数,
所以$h(k)≥5+\frac{1}{2}[|2a+5|+|2a-5|]=5+2a$
②当$0≤a<\frac{5}{2}$时,$k≥f(a)=7a-\frac{25}{4}$,
${x_1}=\frac{{-5-\sqrt{25+4k+12a}}}{2},{x_2}=\frac{{5+\sqrt{25+4k-28a}}}{2}$
$\begin{array}{l}∴|{x_1}-{x_2}{|_{max}}={x_2}-{x_1}=\frac{{5+\sqrt{25+4k-28a}}}{2}-\frac{{-5-\sqrt{25+4k+12a}}}{2}\\=5+\frac{1}{2}[\sqrt{25+4k-28a}+\sqrt{25+4k+12a}]=h(k)\end{array}$
因为h(k)关于k为增函数,所以$h(k)≥5+\sqrt{10a}$
综上:$h(k)=\left\{\begin{array}{l}5+\frac{1}{2}[\sqrt{25+4k-28a}+\sqrt{25+4k+12a}],k≥{a^2}+2a,a≥\frac{5}{2}\\ 5+\frac{1}{2}[\sqrt{25+4k-28a}+\sqrt{25+4k+12a}],k≥7a-\frac{25}{4},0≤a≤\frac{5}{2}\end{array}\right.$
所以当$0≤a≤\frac{5}{2}$时,$h(k)∈\sqrt{10a}+5$,
当$a≥\frac{5}{2}$时,h(k)≥2a+5.
点评 本题考查的知识点是分段函数的应用,二次函数的图象和性质,是分类函数与二次函数的综合应用,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2kπ,2kπ+π)k∈Z | B. | (2kπ,2kπ+2π)k∈Z | C. | (kπ,kπ+$\frac{π}{2}$)k∈Z | D. | (kπ+$\frac{π}{2}$,kπ+π)k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
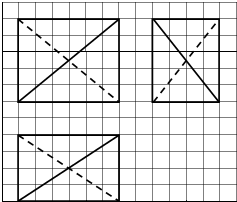 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某多面件的三视图,该多面体的体积为( )| A. | 40cm3 | B. | 50cm3 | C. | 60cm3 | D. | 80cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧¬q | C. | ¬p∧q | D. | p∧¬q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com