
分析 由$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$列出方程求出a的值,根据求导法则求出$[\frac{f(x)}{g(x)}]′$,结合条件判断出导数的符号,即可确定函数的单调性,由指数函数的单调性确定a的值,代入$\frac{f(n)}{g(n)}$由条件和等比数列的前n项和公式求出n的值.
解答 解:因为$\frac{f(x)}{g(x)}$=ax,且$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$,
所以a+${a}^{-1}=\frac{5}{2}$,化简得2a2-5a+2=0,解得a=$\frac{1}{2}$或2,
因为f′(x)g(x)<f(x)g′(x),
所以$[\frac{f(x)}{g(x)}]′$=$\frac{f′(x)g(x)-f(x)g′(x)}{{g}^{2}(x)}$<0,
则$\frac{f(x)}{g(x)}={a}^{x}$在定义域上单调递减,故a=$\frac{1}{2}$,
所以$\frac{f(n)}{g(n)}$=${(\frac{1}{2})}^{n}$,则有穷数列{$\frac{f(n)}{g(n)}$}(n∈N•)是以$\frac{1}{2}$为首项、公比的等比数列,
因为有穷数列{$\frac{f(n)}{g(n)}$}(n∈N•)的前n项和等于$\frac{63}{64}$,
所以$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}=\frac{63}{64}$,解得n=6,
故答案为:6.
点评 本题考查了等比数列的定义、前n项和公式,以及函数的导数与函数单调性关系,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
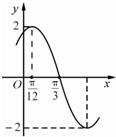 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
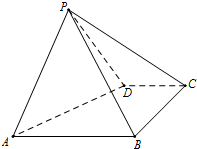 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬p) | B. | ¬((¬p)∧(¬p)) | C. | (¬p)∧(¬p) | D. | ¬(p∨p) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com