
【题目】2019年7月,超强台风登陆某地区.据统计,本次台风造成该地区直接经济损失119.52亿元.经过调查住在该地某小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
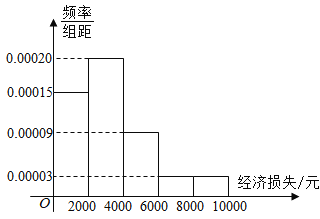
(1)根据频率分布直方图估计小区平均每户居民的平均损失;
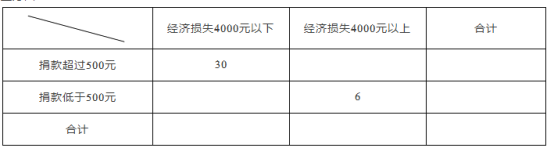
(2)台风后区委会号召小区居民为台风重灾区捐款,经过调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(3)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由王师傅和张师傅两人进行维修,王师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求王师傅比张师傅早到小区的概率.
附:临界值表

参考公式: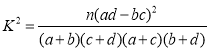 ,
,![]() .
.
【答案】(1)3360;(2)有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关;(3)
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关;(3)![]()
【解析】
(1)根据由频率分布直方图计算平均数的方法,计算出平均损失.
(2)根据已知条件填写![]() 列联表,计算出
列联表,计算出![]() 的值,由此判断出有
的值,由此判断出有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关.
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关.
(3)利用面积型几何概型的概率计算方法,计算出所求概率.
(1)记每户居民的平均损失为![]() 元,则:
元,则:
![]()
(2)如图:
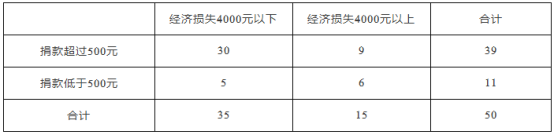
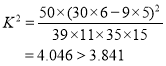 ,
,
所以有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关.
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关.
(3)设王师傅,张师傅到小区的时间分别为![]() ,则
,则![]() 可以看成平面中的点.
可以看成平面中的点.
试验的全部结果所构成的区域为![]() ,则
,则![]() ,事件
,事件![]() 表示王师傅比张师傅早到小区,所构成的区域为
表示王师傅比张师傅早到小区,所构成的区域为![]() ,
,
即图中的阴影部分:面积![]() ,所以
,所以![]() ,
,
∴王师傅比张师傅早到小区的概率是![]() .
.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 的图象在
的图象在![]() 处取得极值4.
处取得极值4.
(1)求函数![]() 的单调区间;
的单调区间;
(2)对于函数![]() ,若存在两个不等正数
,若存在两个不等正数![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,则把区间
,则把区间![]() 叫函数
叫函数![]() 的“正保值区间”.问函数
的“正保值区间”.问函数![]() 是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两陶瓷厂生产规格为![]() 的矩形瓷砖(长和宽都约为
的矩形瓷砖(长和宽都约为![]() ) ,根据产品出厂检测结果,每片瓷砖质量
) ,根据产品出厂检测结果,每片瓷砖质量![]() (单位:
(单位:![]() )在
)在![]() 之间的称为正品,其余的作为废品直接回炉处理.正品瓷
之间的称为正品,其余的作为废品直接回炉处理.正品瓷
砖按行业生产标准分为“优等”、“一级”、“合格”三个标准,主要按照每片瓷砖的“尺寸误差”加以划分,每片价格分别为![]() 元、
元、![]() 元、
元、![]() 元.若规定每片正品瓷砖的“尺寸误差”计算方式为,设矩形瓷砖的长与宽分别为
元.若规定每片正品瓷砖的“尺寸误差”计算方式为,设矩形瓷砖的长与宽分别为![]() (单位:
(单位:![]() ) ,则“尺寸误差”为
) ,则“尺寸误差”为![]() ,“优等”瓷砖的“尺寸误差”范围是
,“优等”瓷砖的“尺寸误差”范围是![]() ,“一级”瓷砖的“尺寸误差”范围是
,“一级”瓷砖的“尺寸误差”范围是![]() ,“合格”瓷砖的“尺寸误差”范围是
,“合格”瓷砖的“尺寸误差”范围是![]() .现分别从甲、乙两厂生产的正品瓷砖中随机抽取
.现分别从甲、乙两厂生产的正品瓷砖中随机抽取![]() 片瓷砖,相应的“尺寸误差”组成的样本数据如下:
片瓷砖,相应的“尺寸误差”组成的样本数据如下:
(甲厂产品的“尺寸误差”频数表)
尺寸误差 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(乙厂产品的“尺寸误差”柱状图)

(1)根据样本数据分别计算甲、乙两厂生产的正品瓷砖的“尺寸误差”的平均值;
(2)若用这个样本的频率分布估计总体分布,求乙厂所生产的正品瓷砖的平均价格;
(3)现用分层抽样的方法从甲厂生产的![]() 片样本瓷砖中随机抽取
片样本瓷砖中随机抽取![]() 片,再从抽取的
片,再从抽取的![]() 片瓷砖中的“一级”瓷砖与“合格”瓷砖中随机选.取
片瓷砖中的“一级”瓷砖与“合格”瓷砖中随机选.取![]() 片进一步分析其“平整度”,求这
片进一步分析其“平整度”,求这![]() 片瓷砖的价格之和大于
片瓷砖的价格之和大于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线
轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,写出直线
的极坐标方程化为直角坐标方程,写出直线![]() 的参数方程的标准形式;
的参数方程的标准形式;
(2)已知直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以
,以![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .已知
.已知![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,若
为顶角的等腰直角三角形,若![]() 在直线
在直线![]() 的右下方,求
的右下方,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com