
分析 (Ⅰ)通过讨论x的范围,求出不等式的解集即可;(Ⅱ)求出f(x)的最小值,得到关于a的不等式,解出即可.
解答 解:(Ⅰ)不等式f(x)<6,即|x+2|+|x-3|<6,可化为
①$\left\{\begin{array}{l}{x≤-2}\\{-({x+2})-({x-3})<6}\end{array}$或②$\left\{\begin{array}{l}{-2<x<3}\\{({x+2})-({x-3})<6}\end{array}$或③$\left\{\begin{array}{l}{x≥3}\\{({x+2})+({x-3})<6}\end{array}$
解①得$-\frac{5}{2}<x≤-2$,解②得-2<x<3,解③得$3≤x<\frac{7}{2}$,
综合得$-\frac{5}{2}<x<\frac{7}{2}$,即原不等式的解集为$\{x|-\frac{5}{2}<x<\frac{7}{2}\}$. …6分
(Ⅱ)因为f(x)=|x+2|+|x-3|≥|(x+2)-(x-3)|=5,
当且仅当-2≤x≤3时,等号成立,即f(x)min=5,
又关于的不等式f(x)≥|2a+1|恒成立,则|2a+1|≤5,
解得-3≤a≤2,即实数的取值范围为[-3,2].…12分.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,转化思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三个内角都不大于 60° | B. | 三个内角至多有一个大于 60° | ||
| C. | 三个内角都大于60° | D. | 三个内角至多有两个大于 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y-1=0 | B. | x-2y+1=0 | C. | 2x+y-2=0 | D. | x+2y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
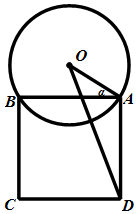 某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)
某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com