Question

【题目】某校举办了一场主题为“爱诗词、爱祖国”的诗词知识竞赛，从参赛的全体学生中抽出30人的成绩作为样本.对这30名学生的成绩进行统计，并按、、、、、分组，得到如图所示的频率分布直方图.

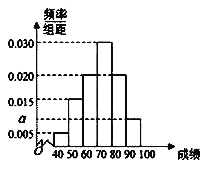
（1）求图中实数的值；

（2）估计参加这次知识竞赛的学生的平均成绩及成绩的中位数（平均成绩用每组中点值做代表，结果均保留一位小数）.

Answer 1

【答案】（1）；（2）平均成绩为分，成绩的中位数为分.

【解析】

（1）利用频率分布直方图的所有矩形的面积之和为可求得实数的值；

（2）将每个矩形底边的中点值乘以矩形的面积，再将所得结果相加即可得出样本数据的平均数，利用中位数左边的矩形面积之和为可求得中位数的值.

（1），；

（2）平均数，

所以，估计参赛学生的平均成绩为分.

设样本数据的中位数为，由知，

，解得，

所以，估计参加这次知识竞赛的学生成绩的中位数约为分.