
【题目】已知奇函数![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,则不等式
,则不等式![]() 的解集________.
的解集________.
【答案】![]()
【解析】
根据题意,由奇函数的性质可得f(﹣3)=0,结合函数的单调性分析可得f(x)>0与f(x)<0的解集,又由(x﹣1)f(x)>0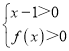 或
或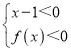 ,分析可得x的取值范围,即可得答案.
,分析可得x的取值范围,即可得答案.
根据题意,f(x)为奇函数且f(3)=0,则f(﹣3)=0,
又由f(x)在(﹣∞,0)上单调递减,则在(﹣∞,﹣3)上,f(x)>0,在(﹣3,0)上,f(x)<0,
又由f(x)为奇函数,则在(0,3)上,f(x)>0,在(3,+∞)上,f(x)<0,
则f(x)<0的解集为(﹣3,0)∪(3,+∞),f(x)>0的解集为(﹣∞,﹣3)∪(0,3);
(x﹣1)f(x)>0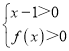 或
或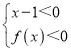 ,
,
分析可得:﹣1<x<0或1<x<3,
故不等式的解集为(﹣3,0)∪(1,3);
故答案为(﹣3,0)∪(1,3);


科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1-20这20个整数中随机选择一个数,设事件A表示选到的数能被2整除,事件B表示选到的数能被3整除,求下列事件的概率;
(1)这个数既能被2整除也能被3整除;
(2)这个数能被2整除或能被3整除;
(3)这个数既不能被2整除也不能被3整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|2x-1≥1},B={x|x2-4x-5<0}.
(Ⅰ)求A∩B,(UA)∪(UB);
(Ⅱ)设集合C={x|m+1<x<2m-1},若B∩C=C,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(I)应收集多少位男生样本数据?
(II)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,试估计该校学生每周平均体育运动时间超过4个小时的概率;
,试估计该校学生每周平均体育运动时间超过4个小时的概率;

(Ⅲ)在样本数据中,有165位男生的每周平均体育运动时间超过4个小时请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() %的把握认为“该校学生的每周平均体育运动时间与性别有关”.
%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
男生 | 女士 | 总计 | |
每周平均体育运动时 间不超过4小时 | |||
每周平均体育运动时 间超过4小时 | |||
总计 |
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年俄罗斯世界杯将于2018年6月14日至7月15日在俄罗斯境内![]() 座城市的
座城市的![]() 座球场内举行,共有
座球场内举行,共有![]() 支球队参加比赛,其中欧洲有
支球队参加比赛,其中欧洲有![]() 支球队参赛,中北美球队有
支球队参赛,中北美球队有![]() 支球队参赛,亚洲、南美洲、非洲各有
支球队参赛,亚洲、南美洲、非洲各有![]() 支球队参赛,所有参赛球队被平均分入
支球队参赛,所有参赛球队被平均分入![]() 个小组.已知
个小组.已知![]() 小组的
小组的![]() 支队伍来自不同的大洲,东道主俄罗斯(俄罗斯属于欧洲球队)和墨西哥(墨西哥属于中北美球队)在
支队伍来自不同的大洲,东道主俄罗斯(俄罗斯属于欧洲球队)和墨西哥(墨西哥属于中北美球队)在![]() 小组中,那么南美洲球队巴西队在
小组中,那么南美洲球队巴西队在![]() 小组的概率为( )
小组的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:(1)正方形的四条边相等;(2)有两个角是![]() 的三角形是等腰直角三角形;(3)正数的平方根不等于0;(4)至少有一个正整数是偶数;是全称量词命题的有________;是存在量词命题的有________.(填序号)
的三角形是等腰直角三角形;(3)正数的平方根不等于0;(4)至少有一个正整数是偶数;是全称量词命题的有________;是存在量词命题的有________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com