
 | A | B | C |
| �� | 4 | 8 | 3 |
| �� | 5 | 5 | 10 |
���� ��1������ԭ�ϵĶ����г�����ʽ�飬����ƽ������
��2��������z=2x+3y����y=-$\frac{2}{3}x+\frac{z}{3}$����Ͽ������ҳ����Ž��λ�ã��з����������Ž⣮
��� �⣺��1��x��y�����������ϵʽΪ��$\left\{\begin{array}{l}{4x+5y��200}\\{8x+5y��360}\\{3x+10y��300}\\{x��N}\\{y��N}\end{array}\right.$��
����ƽ��������ͼ��ʾ��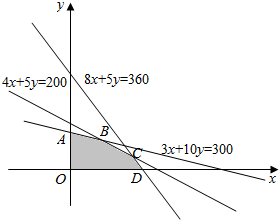
��2��������Ϊz��Ԫ����z=2x+3y��
��y=-$\frac{2}{3}$x+$\frac{z}{3}$��
�൱ֱ��y=-$\frac{2}{3}$x+$\frac{z}{3}$������Bʱ���ؾ�$\frac{z}{3}$���z���
�ⷽ����$\left\{\begin{array}{l}{4x+5y=200}\\{3x+10y=300}\end{array}\right.$��B��20��24����
��z�����ֵΪ2��20+3��24=112��
�𣺵��������ַ���20��Ƥ�����ַ���24��Ƥʱ����������������Ϊ112��Ԫ��
���� ���⿼���˼����Թ滮��Ӧ�ã�������������ͼ�����������������е��⣮


 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 5 | C�� | 4 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
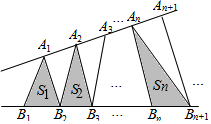
| A�� | {Sn}�ǵȲ����� | B�� | {Sn2}�ǵȲ����� | C�� | {dn}�ǵȲ����� | D�� | {dn2}�ǵȲ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������P-ABCD�ĵ���Ϊ�����Σ�PD��ƽ��ABCD��MΪPC�е㣮
��ͼ������P-ABCD�ĵ���Ϊ�����Σ�PD��ƽ��ABCD��MΪPC�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com