
分析 (1)由三人中恰有一人遇到堵车的概率是$\frac{5}{18}$,得$\frac{2}{3}×\frac{1}{3}×p$+$\frac{1}{3}×\frac{2}{3}×p$+$\frac{1}{3}×\frac{1}{3}×(1-p)$=$\frac{5}{18}$,由此能求出p.
(2)由题意知ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 解:(1)∵择线路A,旅行中遇到堵车的概率是$\frac{2}{3}$,不堵车的概率是$\frac{1}{3}$,
选择线路B,旅行中遇到堵车的概率是p,不堵车的概率是1-p,
甲、乙两人选择线路A,丙选择线路B.且三人在旅行中是否堵车互不影响.
三人中恰有一人遇到堵车的概率是$\frac{5}{18}$,
∴$\frac{2}{3}×\frac{1}{3}×p$+$\frac{1}{3}×\frac{2}{3}×p$+$\frac{1}{3}×\frac{1}{3}×(1-p)$=$\frac{5}{18}$,
解得p=$\frac{1}{2}$.
(2)由题意知ξ的可能取值为0,1,2,3,
P(ξ=0)=$\frac{1}{3}×\frac{1}{3}×\frac{1}{2}$=$\frac{1}{18}$,
P(ξ=1)=$\frac{5}{18}$,
P(ξ=2)=$\frac{1}{3}×\frac{2}{3}×\frac{1}{2}+\frac{2}{3}×\frac{1}{3}×\frac{1}{2}+\frac{2}{3}×\frac{2}{3}×\frac{1}{2}$=$\frac{8}{18}$,
P(ξ=3)=$\frac{2}{3}×\frac{2}{3}×\frac{1}{2}$=$\frac{4}{18}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{18}$ | $\frac{5}{18}$ | $\frac{8}{18}$ | $\frac{4}{18}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
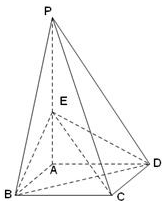 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com