
| A. | $\frac{4}{{π}^{2}}$ | B. | $\frac{2}{π}$+$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{{π}^{2}}$+$\frac{1}{2}$ |
分析 根据几何概型的概率公式,结合积分的应用求出对应的面积即可得到结论.
解答 解:此题为几何概型,事件A的度量为函数y=cosx的图象在[-$\frac{π}{2}$,$\frac{π}{2}$]内与x轴围成的图形的面积,
即2${∫}_{0}^{\frac{π}{2}}$cosxdx=2sinx|${\;}_{0}^{\frac{π}{2}}$=2,
则事件A的概率为P(A)=$\frac{2}{{π}^{2}}$+$\frac{π•\frac{π}{2}}{{π}^{2}}$=$\frac{2}{{π}^{2}}$+$\frac{1}{2}$.
故选:D.
点评 本题主要考查几何概型的概率计算以及利用积分求面积,要求熟练掌握几何概型的求解方法.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | $({2,\frac{2π}{3}})$ | B. | (2,3) | C. | $({2,\frac{5π}{6}})$ | D. | $({2,\frac{3π}{4}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
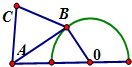 如图,半圆O的直径为1,A为直径延长线上的一点,OA=1,B为半圆上任意一点,以AB为一边作等边三角形ABC,则四边形OACB面积的最大值为$\frac{5\sqrt{3}}{16}$+$\frac{1}{2}$.
如图,半圆O的直径为1,A为直径延长线上的一点,OA=1,B为半圆上任意一点,以AB为一边作等边三角形ABC,则四边形OACB面积的最大值为$\frac{5\sqrt{3}}{16}$+$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com