
已知函数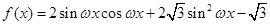 (
(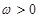 )的最小正周期为
)的最小正周期为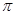 .
.
(Ⅰ)求函数 的单调增区间;
的单调增区间;
(Ⅱ)将函数 的图象向左平移
的图象向左平移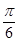 个单位,再向上平移
个单位,再向上平移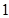 个单位,得到函数
个单位,得到函数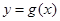 的图象.求
的图象.求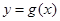 在区间
在区间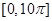 上零点的个数.
上零点的个数.
(Ⅰ)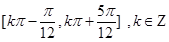 ;(Ⅱ)20.
;(Ⅱ)20.
解析试题分析:(Ⅰ)根据二倍角公式将原式化简成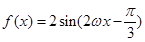 ,而周期
,而周期 ,则
,则 ,
,
从而得出 的解析式
的解析式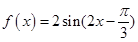 ,将
,将 当成一个整体,则有
当成一个整体,则有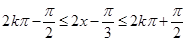 ,解得
,解得 ,故所以函数
,故所以函数 的单调增区间是
的单调增区间是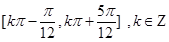 . (Ⅱ)将函数
. (Ⅱ)将函数 的图象向左平移
的图象向左平移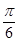 个单位,再向上平移1个单位,得到
个单位,再向上平移1个单位,得到 的图象,即
的图象,即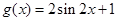 ,令
,令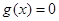 ,得:
,得: 或
或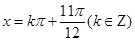 ,
,
易知每个周期上恰好有两个零点,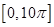 恰为
恰为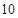 个周期,故
个周期,故 在
在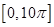 上有
上有 个零点.
个零点.
试题解析:(Ⅰ)由题意得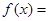


由周期为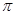 ,得
,得 . 得
. 得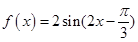
由正弦函数的单调增区间得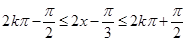 ,得
,得
所以函数 的单调增区间是
的单调增区间是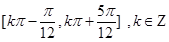 .
.
(Ⅱ)将函数 的图象向左平移
的图象向左平移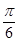 个单位,再向上平移1个单位,
个单位,再向上平移1个单位,
得到 的图象,所以
的图象,所以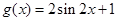
令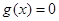 ,得:
,得: 或
或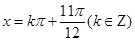
所以函数在每个周期上恰有两个零点,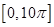 恰为
恰为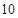 个周期,故
个周期,故 在
在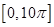 上有
上有 个零点.
个零点.
考点:1.三角函数的化简与性质应用;2.三角函数的图像变换;3.函数的零点.


科目:高中数学 来源: 题型:解答题
已知函数f(x)=sinx+cosx,f′(x)是f(x)的导函数,F(x)=f(x)f′(x)+f2(x)
(Ⅰ)求F(x)的最小正周期及单调区间;
(Ⅱ)求函数F(x)在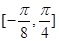 上的值域;
上的值域;
(Ⅲ)若f(x)=2f′(x),求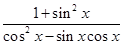 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com