
已知函数f(x)=sinx+cosx,f′(x)是f(x)的导函数,F(x)=f(x)f′(x)+f2(x)
(Ⅰ)求F(x)的最小正周期及单调区间;
(Ⅱ)求函数F(x)在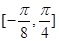 上的值域;
上的值域;
(Ⅲ)若f(x)=2f′(x),求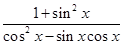 的值.
的值.
(Ⅰ)T=π.单调递增区间: 单调递减区间:
单调递减区间: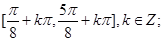
(Ⅱ)[1,1+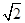 ];(Ⅲ)
];(Ⅲ)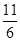 .
.
解析试题分析:(I)将函数F(x)=f(x)f′(x)+f2(x)化一可得:F(x)=1+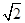 sin(2x+
sin(2x+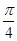 ),由此可得F(x)的最小正周期及单调区间.(Ⅱ) 由
),由此可得F(x)的最小正周期及单调区间.(Ⅱ) 由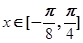 得
得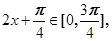 这样可得sin(2x+
这样可得sin(2x+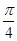 )的范围,从而得函数F(x)的值域.
)的范围,从而得函数F(x)的值域.
(Ⅲ)由f(x)=2f′(x),得:sinx+cosx=2cosx-2sinx,由此可得tanx的值.
将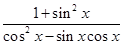 化为只含tanx式子,将tanx.的值代入即可.
化为只含tanx式子,将tanx.的值代入即可.
试题解析:(I)∵f′(x)=cosx-sinx,
∴F(x)=f(x)f′(x)+f2(x)=cos2x-sin2x+1+2sinxcosx=1+sin2x+cos2x=1+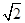 sin(2x+
sin(2x+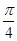 ),
),
最小正周期为T=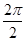 =π.
=π.
单调递增区间: 单调递减区间:
单调递减区间: 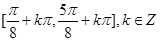 . 4分
. 4分
(Ⅱ)由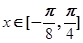 得
得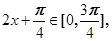
所以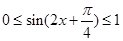 ,所以函数F(x)的值域为[1,1+
,所以函数F(x)的值域为[1,1+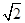 ]. 8分
]. 8分
(Ⅲ)∵f(x)=2f′(x), ∴sinx+cosx=2cosx-2sinx,
∴cosx=3sinx, ∴tanx=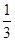 ,
,
∴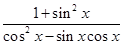 =
=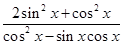 =
=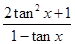 =
=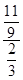 =
=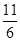 . 13分
. 13分
考点:1、三角变换;2、三角函数的单调性和范围;3、三角函数同角关系式.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
已知函数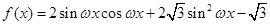 (
(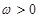 )的最小正周期为
)的最小正周期为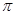 .
.
(Ⅰ)求函数 的单调增区间;
的单调增区间;
(Ⅱ)将函数 的图象向左平移
的图象向左平移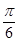 个单位,再向上平移
个单位,再向上平移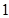 个单位,得到函数
个单位,得到函数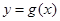 的图象.求
的图象.求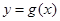 在区间
在区间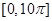 上零点的个数.
上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知向量a=(2cosx,2sinx),b=(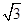 cosx,cosx),设函数f(x)=a•b-
cosx,cosx),设函数f(x)=a•b-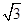 ,求:
,求:
(1)f(x)的最小正周期和单调递增区间;
(2)若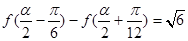 , 且α∈(
, 且α∈( ,π). 求α.
,π). 求α.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com