
已知函数 ,若
,若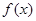 的最大值为1
的最大值为1
(Ⅰ)求 的值,并求
的值,并求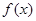 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,角
中,角 、
、 、
、 的对边
的对边 、
、 、
、 ,若
,若 ,且
,且 ,试判断三角形的形状.
,试判断三角形的形状.
(Ⅰ) ,
, ; (Ⅱ)△ABC为直角三角形.
; (Ⅱ)△ABC为直角三角形.
解析试题分析:(Ⅰ)若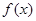 的最大值为1,求
的最大值为1,求 的值,并求
的值,并求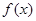 的单调递减区间,需将
的单调递减区间,需将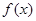 化成一个角的一个三角函数,因此须对
化成一个角的一个三角函数,因此须对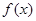 进行整理,可利用两角或与差的三角函数公式展开得到
进行整理,可利用两角或与差的三角函数公式展开得到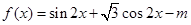 ,然后利用两角和与差的三角函数公式整理成
,然后利用两角和与差的三角函数公式整理成 ,利用
,利用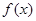 的最大值为1,来确定
的最大值为1,来确定 的值,并求得
的值,并求得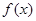 的单调递减区间;(Ⅱ)判断三角形的形状,由
的单调递减区间;(Ⅱ)判断三角形的形状,由 ,可求出角B的值,由已知
,可求出角B的值,由已知 ,利用正弦定理将边化成角,由于
,利用正弦定理将边化成角,由于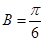 ,则
,则 ,即
,即 ,从而求出
,从而求出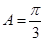 ,这样就判断出三角形的形状.
,这样就判断出三角形的形状.
试题解析:(Ⅰ)由题意可得 (3分)
(3分) ,所以
,所以 , (4分)
, (4分)
令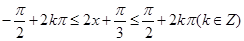 ,解不等式可得单调增区间为
,解不等式可得单调增区间为 (6分)
(6分)
(Ⅱ)因为 , 则
, 则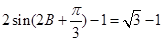 ,
,  , ∵
, ∵ ,
,
∴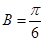 (8分)
(8分)
又 ,则
,则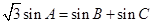 ,
,
∴ (10分)
(10分)
∴ ,所以
,所以 ,故△ABC为直角三角形 (12分)
,故△ABC为直角三角形 (12分)
考点:两角和正弦公式,正弦函数的单调性与最值,根据三角函数的值求角,解三角形.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=sinx+cosx,f′(x)是f(x)的导函数,F(x)=f(x)f′(x)+f2(x)
(Ⅰ)求F(x)的最小正周期及单调区间;
(Ⅱ)求函数F(x)在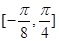 上的值域;
上的值域;
(Ⅲ)若f(x)=2f′(x),求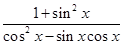 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com