
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{π}{8}$ |
分析 首先分析题目求这两个数的平方和也在区间[0,2]内的概率,可以联想到用几何的方法求解,利用面积的比值直接求得结果.
解答 解:将取出的两个数分别用x,y表示,则x,y∈[0,2]
要求这两个数的平方和也在区间[0,2]内,即要求0≤x2+y2≤2,
故此题可以转化为求0≤x2+y2≤2在区域$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤2}\end{array}\right.$内的面积比的问题.
即由几何知识可得到概率为$\frac{\frac{1}{4}π•2}{{2}^{2}}$=$\frac{π}{8}$;
故选:D.
点评 此题考查等可能时间概率的问题,利用几何概型的方法解决本题,概率知识在高考中难度有所下降,对利用古典概型和几何概型的基本方法要熟练掌握.


科目:高中数学 来源: 题型:选择题
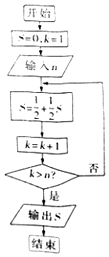
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 3 | C. | $\frac{9}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
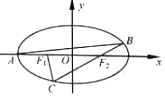 如图,设点A,F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左,右焦点,过点A作斜率为k的直线交椭圆于另一点B,连接BF2并延长交椭圆于点C.
如图,设点A,F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左顶点和左,右焦点,过点A作斜率为k的直线交椭圆于另一点B,连接BF2并延长交椭圆于点C.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
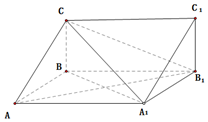 如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.
如图,三棱柱ABC-A1B1C1中,四边形AA1BB1是菱形,∠BB1A1=$\frac{π}{3},{C_1}{B_1}⊥面A{A_1}B{B_1}$,二面角C-A1B1-B为$\frac{π}{6}$,CB=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com