(Ⅰ)因为
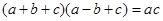
,所以

.
由余弦定理得

,
因此

.
(Ⅱ)由(Ⅰ)知

,所以





,
故

或

,
因此

或

.
(1)因给出了边的关系,首选利用余弦定理进行转化;(2)利用第一问的结论,借助三角公式进行化简求值.利用正弦定理与余弦定理解题,经常利用转化思想,一个是边转化为角,另一个是角转化为边.具体情况应根据题目给定的表达式进行确定,不管哪个途径,最终转化为角的统一或边的统一,也是我们利用正余弦定理化简式子的最终目的.对于两个定理都能用的题目,应优先考虑利用正弦定理,会给计算带来相对的简便.根据已知条件中边的大小来确定角的大小,此时利用正弦定理去计算较小边所对的角,可避免分类讨论;利用余弦定理的推论,可根据角的余弦值的正负直接确定所求角是锐角还是钝角,但是计算麻烦.
【考点定位】本题考查余弦定理、两角和与差的公式以及求角问题,考查学生的划归能力和计算能力.

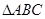 的内角A、B、C的对边分别为a、b、c,
的内角A、B、C的对边分别为a、b、c,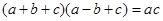 .
.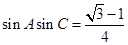 ,求C.
,求C. (Ⅱ)
(Ⅱ) 或
或
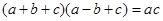 ,所以
,所以 .
. ,
, .
. ,所以
,所以



 ,
, 或
或 ,
, 或
或 .
.
