
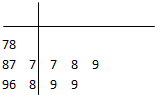
 学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
| ||
|
| ||||
|
| 49 |
| 60 |
| 7 |
| 10 |
| 342 |
| 1000 |
| C | 1 3 |
| 3 |
| 10 |
| 7 |
| 10 |
| 441 |
| 1000 |
| C | 2 3 |
| 3 |
| 10 |
| 7 |
| 10 |
| 189 |
| 1000 |
| 3 |
| 10 |
| 27 |
| 1000 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 342 |
| 1000 |
| 441 |
| 1000 |
| 189 |
| 1000 |
| 27 |
| 1000 |


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| m |
| a |
| b |
| n |
| a |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 发车时间 | 8:10 | 8:30 | 8:50 | 9:10 | 9:30 | 9:50 | ||||||||||||
| 概率 |
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
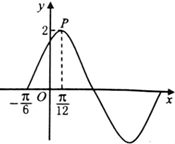 已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,| π |
| 2 |
| 3π |
| 2 |
| α |
| 2 |
| 5π |
| 12 |
| 12 |
| 13 |
| α |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 6 |

| AP |
| AQ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com