
| A. | [1,1+$\sqrt{2}$] | B. | [2-$\sqrt{2}$,2+$\sqrt{2}$] | C. | [$\sqrt{2},2\sqrt{2}$] | D. | [3-2$\sqrt{2}$,3+2$\sqrt{2}$] |
分析 由$\overrightarrow{a}$,$\overrightarrow{b}$是单位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=0.可设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(x,y).由向量$\overrightarrow{c}$满足|$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=2,可得(x-1)2+(y-1)2=4.其圆心C(1,1),半径r=2.利用|OC|-r≤|$\overrightarrow{c}$|=$\sqrt{{x}^{2}{+y}^{2}}$≤|OC|+r即可得出.
解答 解:由$\overrightarrow{a}$,$\overrightarrow{b}$是单位向量,$\overrightarrow{a}$•$\overrightarrow{b}$=0,
可设$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=(x,y),
由向量$\overrightarrow{c}$满足|$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=2,
∴|(x-1,y-1)|=2,
∴$\sqrt{{(x-1)}^{2}{+(y-1)}^{2}}$=2,即(x-1)2+(y-1)2=4,
其圆心C(1,1),半径r=2,
∴|OC|=$\sqrt{2}$
∴2-$\sqrt{2}$≤|$\overrightarrow{c}$|=$\sqrt{{x}^{2}{+y}^{2}}$≤2+$\sqrt{2}$.
故选:B.
点评 本题考查了向量的垂直与数量积的关系、数量积的运算性质、点与圆上的点的距离大小关系,考查了推理能力和计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
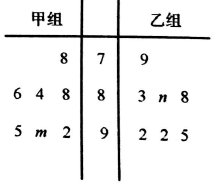 某中学奥数培训班共有14人,分为两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则n-m的值( )
某中学奥数培训班共有14人,分为两个小组,在一次阶段测试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则n-m的值( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0$<\frac{r}{L}<\frac{1}{2}$ | B. | $\frac{1}{2}≤\frac{r}{L}<1$ | C. | 0$<\frac{r}{L}<\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}≤\frac{r}{L}<1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com