考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)连接AC交BD于O,连接EO,C1O,证明EO⊥平面BDC1,即可证明平面EBD⊥平面C1BD;
(Ⅱ)设EC与AC1交点为F,则四棱锥E-ABCD与四棱锥C1-ABCD公共部分为四棱锥F-ABCD,即可得出结论.
解答:
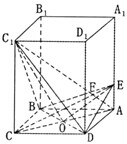
(Ⅰ)证明:连接AC交BD于O,连接EO,C
1O,
∵四边形ABCD为正方形,AB=2
,
∴AC=4,AO=
AC=2,
∵A
1A=4,AE=3EA,
∴EA=1,
∴tan∠EOA=
,tan∠C
1OC=2,
∴∠EOA+∠C
1OC=90°,
∴EO⊥OC
1,
∵ED=3,EB=3,
∴ED=EB,
∴在△EBD中,EO⊥BD
∴EO⊥平面BDC
1.
又EO?平面BDE
∴平面C
1BD⊥平面BDE.
(Ⅱ)解:设EC与AC
1交点为F,则四棱锥E-ABCD与四棱锥C
1-ABCD公共部分为四棱锥F-ABCD,
在矩形A
1ACC
1中,
==4,∴
=
,
∴F到AC的距离d=
AE=
,
∴F到平面ABCD的距离为
,
∴四棱锥F-ABCD的高为
,
∴V
F-ABCD=
•(2)2•=
,
∴四棱锥E-ABCD与四棱锥C
1-ABCD公共部分的体积为
.
点评:本题考查的知识点是平面与平面垂直的判定,体积的计算,其中熟练掌握面面垂直的判定定理及证明步骤是解答本题的关键.

 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1⊥底面ABCD,AB=2
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1⊥底面ABCD,AB=2 (Ⅰ)证明:连接AC交BD于O,连接EO,C1O,
(Ⅰ)证明:连接AC交BD于O,连接EO,C1O,


 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.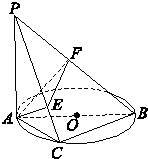 如图所示,已知PA⊥⊙O所在平面,AB是⊙O的直径,点C是⊙O上任意一点,过A作AE⊥PC于点E,AF⊥PB于点F,求证:
如图所示,已知PA⊥⊙O所在平面,AB是⊙O的直径,点C是⊙O上任意一点,过A作AE⊥PC于点E,AF⊥PB于点F,求证: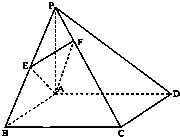 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,BC=
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,BC=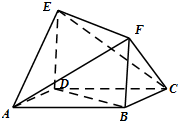 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=