
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 总计 | |
| 物理成绩优秀 | 5 | 2 | 7 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 总计 | 6 | 14 | 20 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
分析 (1)根据题意,完成 2×2 列联表;
(2)根据表中数据,计算K2,对照临界值得出结论.
解答 解:(1)根据题意,完成 2×2 列联表如下;
| 数学成绩优秀 | 数学成绩不优秀 | 总计 | |
| 物理成绩优秀 | 5 | 2 | 7 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 总计 | 6 | 14 | 20 |
点评 本题考查了列联表与独立性检验的应用问题,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-∞,1]∪[2,+∞) | C. | (-∞,3]∪[6,+∞) | D. | (3,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
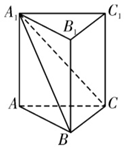 在我国古代数学名著《九章算术》中将底面为直角三角形,且侧棱垂直于底面的三棱柱称之为堑堵,如图,在堑堵ABC-A1B1C1中,AB=BC,AA1>AB,堑堵的顶点C1到直线A1C的距离为m,C1到平面A1BC的距离为n,则$\frac{m}{n}$的取值范围是( )
在我国古代数学名著《九章算术》中将底面为直角三角形,且侧棱垂直于底面的三棱柱称之为堑堵,如图,在堑堵ABC-A1B1C1中,AB=BC,AA1>AB,堑堵的顶点C1到直线A1C的距离为m,C1到平面A1BC的距离为n,则$\frac{m}{n}$的取值范围是( )| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | ($\frac{\sqrt{2}}{2}$,$\frac{2\sqrt{3}}{3}$) | C. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{3}$) | D. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |f(x)-f(a)|≤3|a|+3 | B. | |f(x)-f(a)|≤2|a|+4 | C. | |f(x)-f(a)|≤|a|+5 | D. | |f(x)-f(a)|≤2(|a|+1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 喜欢 | 40 | 20 | 60 |
| 不喜欢 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别无关” | |
| C. | 有99%以上的把握认为“喜欢该节目与性别有关” | |
| D. | 有99%以上的把握认为“喜欢该节目与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
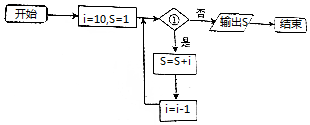
| A. | (5,6] | B. | [5,6) | C. | (6,7] | D. | [6,7) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com