
分析 从四个函数中任选2个,基本事件总数n=${C}_{4}^{2}=6$,再利用列举法求出事件A:“所选2个函数的图象有且只有一个公共点”包含的基本事件的个数,由此能求出事件A:“所选2个函数的图象有且只有一个公共点”的概率.
解答 解:给出四个函数:①y=-x,②y=-$\frac{1}{x}$,③y=x3,④y=x${\;}^{\frac{1}{2}}$,
从四个函数中任选2个,基本事件总数n=${C}_{4}^{2}=6$,
③④有两个公共点(0,0),(1,1).
事件A:“所选2个函数的图象有且只有一个公共点”包含的基本事件有:
①③,①④共2个,
∴事件A:“所选2个函数的图象有且只有一个公共点”的概率为P(A)=$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 参会人数x(万人) | 11 | 9 | 8 | 10 | 12 |
| 原材料t(袋) | 28 | 23 | 20 | 25 | 29 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
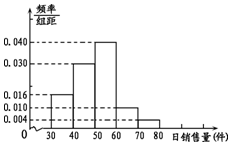 某超市计划销售某种产品,先试销该产品n天,对这n天日销售量进行统计,得到频率分布直方图如图.
某超市计划销售某种产品,先试销该产品n天,对这n天日销售量进行统计,得到频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 总计 | |
| 物理成绩优秀 | 5 | 2 | 7 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 总计 | 6 | 14 | 20 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com