
【题目】2016年春节期间全国流行在微信群里发、抢红包,现假设某人将688元发成手气红包50个,产生的手气红包频数分布表如表:

(I)求产生的手气红包的金额不小于9元的频率;
(Ⅱ)估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)在这50个红包组成的样本中,将频率视为概率.
(i)若红包金额在区间[21,25]内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
(ii)随机抽取手气红包金额在[1,5)∪[﹣21,25]内的两名幸运者,设其手气金额分别为m,n,求事件“|m﹣n|>16”的概率.
【答案】(Ⅰ)![]() ;(Ⅱ)12.44;(Ⅲ)(i)
;(Ⅱ)12.44;(Ⅲ)(i)![]() ,(ii)
,(ii)![]() .
.
【解析】
(Ⅰ)由题意利用互斥事件概率加法公式能求出产生的手气红包的金额不小于9元的频率.
(Ⅱ)先求出手气红包在[1,5)、[5,9)、[9,13)、[13,17)、[17,21)、[21,25]内的频率,由此能求了出手气红包金额的平均数.
(Ⅲ)(i)由题可知红包金额在区间[21,25]内有两人,由此能求出抢得红包的某人恰好是最佳运气手的概率.(ii)由频率分布表可知,红包金额在[1,5)内有3人,在[21,25]内有2人,由此能求出事件“|m﹣n|>16“的概率P(|m﹣n|>16).
(Ⅰ)由题意得产生的手气红包的金额不小于9元的频率:
p![]() ,
,
∴产生的手气红包的金额不小于9元的频率为![]() .
.
(Ⅱ)手气红包在[1,5)内的频率为![]() 0.06,
0.06,
手气红包在[5,9)内的频率为![]() 0.18,
0.18,
手气红包在[9,13)内的频率为![]() 0.34,
0.34,
手气红包在[13,17)内的频率为![]() 0.22,
0.22,
手气红包在[17,21)内的频率为![]() 0.16,
0.16,
手气红包在[21,25]内的频率为![]() 0.04,
0.04,
则手气红包金额的平均数为:
![]() 3×0.06+7×0.18+11÷0.34+15×0.22+19×0.16+23×0.04=12.44.
3×0.06+7×0.18+11÷0.34+15×0.22+19×0.16+23×0.04=12.44.
(Ⅲ)(i)由题可知红包金额在区间[21,25]内有两人,
∴抢得红包的某人恰好是最佳运气手的概率p![]() .
.
(ii)由频率分布表可知,红包金额在[1,5)内有3人,
设红包金额分别为a,b,c,在[21,25]内有2人,
设红包金额分别为x,y,
若m,n均在[1,5)内,有3种情况:(a,b),(a,c),(b,c),
若m,n均在[21,25]内只有一种情况:(x,y),
若m,n分别在[1,5)和[21,25)内,有6种情况,
即(a,x),(a,y),(b,x),(b,y),(c,x),(c,y),
∴基本事件总数n=10,
而事件“|m﹣n|>16“所包含的基本事件有6种,
∴P(|m﹣n|>16)![]() .
.


科目:高中数学 来源: 题型:
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天或每月行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
根据折线图,下列结论正确的是( )
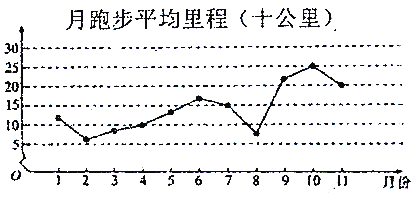
A. 月跑步平均里程的中位数为![]() 月份对应的里程数
月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在![]() 、
、![]() 月
月
D. ![]() 月至
月至![]() 月的月跑步平均里程相对于
月的月跑步平均里程相对于![]() 月至
月至![]() 月,波动性更小,变化比较平稳
月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区平面图如图1所示,![]() 为边界上的点.已知边界
为边界上的点.已知边界![]() 是一段抛物线,其余边界均为线段,且
是一段抛物线,其余边界均为线段,且![]() ,抛物线顶点
,抛物线顶点![]() 到
到![]() 的距离
的距离![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
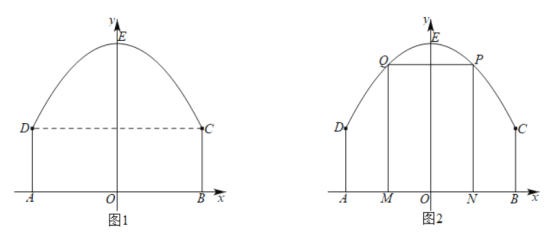
(1)求边界![]() 所在抛物线的解析式;
所在抛物线的解析式;
(2)如图2,该景区管理处欲在区域![]() 内围成一个矩形
内围成一个矩形![]() 场地,使得点
场地,使得点![]() 在边界
在边界![]() 上,点
上,点![]() 在边界
在边界![]() 上,试确定点
上,试确定点![]() 的位置,使得矩形
的位置,使得矩形![]() 的周长最大,并求出最大周长.
的周长最大,并求出最大周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】庄子说:“一尺之锤,日取其半,万世不竭”,这句话描述的是一个数列问题,现用程序框图描述,如图所示,若输入某个正整数n后,输出的S∈(![]() ,
,![]() ),则输入的n的值为( )
),则输入的n的值为( )
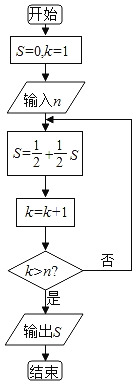
A.7B.6C.5D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的最大面积是
的最大面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆E经过椭圆的左、右焦点,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,
三点共线,![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,且
,且![]() .
.
(i) 求直线![]() 的斜率;
的斜率;
(ii)当![]() 的面积取到最大值时,求直线
的面积取到最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,我国突发新冠肺炎疫情.面对“突发灾难”,举国上下心,继解放军医疗队于除夕夜飞抵武汉,各省医疗队也陆续增援,纷纷投身疫情防控与病人救治之中.为分担“逆行者”的后顾之忧,某大学学生志愿者团队开展“爱心辅学”活动,为抗疫前线工作者子女在线辅导功课.现随机安排甲、乙、丙3名志愿者为某学生辅导数学、物理、化学、生物4门学科,每名志愿者至少辅导1门学科,每门学科由1名志愿者辅导,则数学学科恰好由甲辅导的概率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com