练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．过y2=4x的焦点F作两条弦AB和CD，且AB⊥x轴，|CD|=2|AB|，则弦CD所在直线的方程是x+y+1=0或x+y-1=0．

    分析 根据题意知AB为抛物线的通径进而求出|AB|和|CD|，满足条件的直线CD有两条，验证选项B，把直线和抛物线方程联立，求得x1+x2，进而根据抛物线的定义得出的|CD|符合题意．同样的方法可知x+y-1=0也符合题意．故可得出答案．

    解答 解：依题意知AB为抛物线的通径，|AB|=2p=4，|CD|=2|AB|=8，
    显然满足条件的直线CD有两条，
    由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=x-1}\end{array}\right.$得：x2-6x+1=0，x1+x2=6，此时|CD|=x1+x2+p=8，x+y+1=0符合题意．
    同理，x+y-1=0也符合题意．
    故答案是：x+y+1=0或x+y-1=0．

    点评 本题主要考查了抛物线的性质，直线的一般式方程．属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．在△ABC中，sin2A+sinAsinB=6sin2B．
    （1）求$\frac{BC}{AC}$的值；
    （2）若$cosC=\frac{3}{4}$，求sinB的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点（1，$\frac{3}{2}$），左右焦点为F1、F2，右顶点为A，上顶点为B，且|AB|=$\frac{{\sqrt{7}}}{2}$|F1F2|．
    （1）求椭圆E的方程；
    （2）直线l：y=-x+m与椭圆E交于C、D两点，与以F1、F2为直径的圆交于M、N两点，且$\frac{{\sqrt{7}|CD|}}{|MN|}$=$\frac{36}{7}$，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若函数f（x）=$\left\{\begin{array}{l}\frac{a}{x}，x＞1\\（2-3a）x+1，x≤1\end{array}$是R上的减函数，则实数R的取值范围是 （　　）
    A．$（\frac{2}{3}，1）$B．$[\frac{3}{4}，1）$C．$（\frac{2}{3}，\frac{3}{4}]$D．（$\frac{2}{3}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）=lnx，g（x）=x-$\frac{1}{2}$x2．
    （Ⅰ）若点P是函数f（x）=lnx上任意一点，求点P到直线y=x+1的最小距离；
    （Ⅱ）当x＞e时，求证函数f（x）=lnx的图象位g（x）=x-$\frac{1}{2}$x2图象的上方．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知反比例函数y=$\frac{6}{x}$的图象与正比例函数y=$\frac{2}{3}$x的图象交于A，B两点，B点坐标为（-3，-2），则A点的坐标为（　　）
    A．（-1，-6）B．（1，6）C．（3，2）D．（2，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

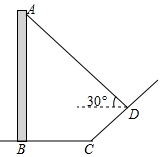    4．如图，直立于地面上的电线杆AB，在阳光下落在水平地面和坡面上的影子分别是BC，CD，测得BC=6米，CD=4米，∠BCD=150°，在D处测得电线杆顶端A的仰角为30°，试求电线杆的高度（结果保留根号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

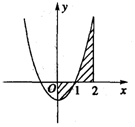    1．由曲线y=x 2-1，直线x=0，x=2和x轴围成的封闭图形的面积（如图）可表示为（　　）
    A．${∫}_{0}^{2}$（x 2-1）dxB．${∫}_{0}^{2}$|（x 2-1）|dx
    C．|${∫}_{0}^{2}$（x 2-1）dx|D．${∫}_{0}^{1}$（x 2-1）dx+${∫}_{1}^{2}$（x 2-1）dx

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知Rt△ABC的顶点分别为A（1，2），B（-1，-2）．，C（1，-2），圆E是△ABC的外接圆．
    （I）求圆E的方程；
    （II）求直线lmx-y-m+1=0被圆E截得的最短弦长及对应的直线l的方程．

    查看答案和解析>>

    同步练习册答案