
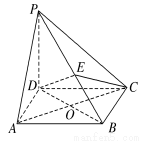
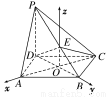
如图,在四棱锥P?ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2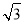 ,E是PB上任意一点.
,E是PB上任意一点.
(1)求证:AC⊥DE;
(2)已知二面角A?PB?D的余弦值为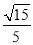 ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.
(1)证明见解析;(2)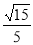 .
.
【解析】
试题分析:
解题思路:(1)利用线面垂直的性质推得线线垂直:(2)建立空间坐标系,利用二面角A?PB?D的余弦值为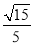 ,求出PD;进而利用空间向量求线面角的正弦值.
,求出PD;进而利用空间向量求线面角的正弦值.
规律总结:对于空间几何体中的垂直、平行关系的判定,要牢牢记住并灵活进行转化,线线关系是关键;涉及夹角、距离问题以及开放性问题,要注意利用空间直角坐标系进行求解.
试题解析:(1)证明:∵PD⊥平面ABCD,AC?平面ABCD,
∴PD⊥AC,
∵四边形ABCD是菱形,∴BD⊥AC,
又BD∩PD=D,∴AC⊥平面PBD,
∵DE?平面PBD,∴AC⊥DE.
(2)在△PDB中,EO∥PD,∴EO⊥平面ABCD,分别以OA,OB,OE所在直线为x轴,y轴,z轴建立空间直角坐标系,设PD=t,则A(1,0,0),B(0,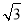 ,0),C(-1,0,0),
,0),C(-1,0,0),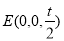 ,P(0,-
,P(0,-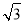 ,t),
,t),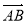 =(-1,
=(-1,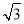 ,0),
,0),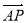 =(-1,-
=(-1,-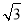 ,t).
,t).
由(1)知,平面PBD的一个法向量为n1=(1,0,0),设平面PAB的法向量为n2=(x,y,z),则根据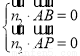 ,
,
得 ,令y=1,得平面PAB的一个法向量为
,令y=1,得平面PAB的一个法向量为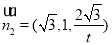
∵二面角A?PB?D的余弦值为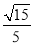 ,
,
则|cos〈n1,n2〉|= ,即
,即
=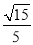 ,解得t=2
,解得t=2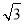 或t=-2
或t=-2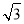 (舍去),
(舍去),
∴P(0,-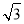 ,2
,2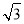 ).
).
设EC与平面PAB所成的角为θ,
∵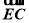 =(-1,0,-
=(-1,0,-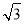 ),n2=(
),n2=(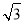 ,1,1),
,1,1),
则sin θ=|cos〈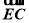 ,n2〉|=
,n2〉|=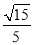 ,
,
∴EC与平面PAB所成角的正弦值为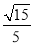 .
.
考点:1.线线垂直的判定;2.空间向量在立体几何中的应用.


科目:高中数学 来源:2015数学一轮复习迎战高考:2-11导数的应用(解析版) 题型:选择题
已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值是( )
A.-37 B.-29 C.-5 D.以上都不对
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考:1-2命题及其关系、充分条件与必要条件(解析版) 题型:选择题
[2013·福建高考]已知集合A={1,a},B={1,2,3},则“a=3”是“A⊆B”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考10-1分类加法计数原理与分步乘法计数原理(解析版) 题型:选择题
[2014·三门峡联考]有4位教师在同一年级的4个班中各教一个班的数学,在数学检测时要求每位教师不能在本班监考,则监考的方法有( )
A.8种 B.9种 C.10种 D.11种
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
函数y=loga(x+3)-1(a>0,且a≠1)的图像恒过定点A,若点A在直线mx+ny+1=0上(其中m,n>0),则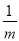 +
+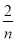 的最小值等于________.
的最小值等于________.
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知圆的极坐标方程为: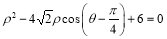 .
.
(1)将极坐标方程化为普通方程;
(2)若点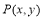 在该圆上,求
在该圆上,求 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com