Question

17．若函数y=m与函数$y=\frac{|x|-1}{{|{x-1}|}}$的图象无公共点，则实数m的取值范围是（-∞，-1）∪（1，+∞）．

Answer 1

分析 作出$y=\frac{|x|-1}{{|{x-1}|}}$的图象，利用函数y=m与函数$y=\frac{|x|-1}{{|{x-1}|}}$的图象无公共点，求出实数m的取值范围．

解答 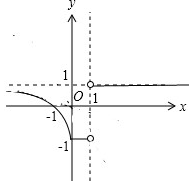解：函数$y=\frac{|x|-1}{{|{x-1}|}}$=$\left\{\begin{array}{l}{\frac{x+1}{x-1}，x≤0}\\{-1，0＜x＜1}\\{1，x＞1}\end{array}\right.$的图象如图所示，
∵函数y=m与函数$y=\frac{|x|-1}{{|{x-1}|}}$的图象无公共点，
∴实数m的取值范围是（-∞，-1）∪（1，+∞）．
故答案为（-∞，-1）∪（1，+∞）．

点评 本题考查函数图象的运用，考查学生分析解决问题的能力，正确作出函数的图象是关键．