
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
分析 运用向量的数量积的定义可得$<\overrightarrow a,\overrightarrow b>={135°}$,不妨设$\overrightarrow a=(1,1)$,$\overrightarrow b=(-1,0)$,设$\overrightarrow c=(x,y)$,运用向量的数量积的加减和数量积的坐标表示,计算即可得到所求最大值.
解答 解:根据题意,向量$|{\overrightarrow a}|=\sqrt{2},|{\overrightarrow b}|=1,|{\overrightarrow c}|=\sqrt{3}$,且$\overrightarrow a•\overrightarrow b=-1$,
可得cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-1}{\sqrt{2}}$,
由于0°≤<$\overrightarrow{a}$,$\overrightarrow{b}$>≤180°,
即有$<\overrightarrow a,\overrightarrow b>={135°}$,不妨设$\overrightarrow a=(1,1)$,$\overrightarrow b=(-1,0)$,
设$\overrightarrow c=(x,y)$,且x2+y2=3,易知$|y|≤\sqrt{3}$
则$\overrightarrow a•\overrightarrow c+\overrightarrow b•\overrightarrow c=(\overrightarrow a+\overrightarrow b)•\overrightarrow c=(0,1)•(x,y)=y≤\sqrt{3}$.
当x=0,y=$\sqrt{3}$时,取得最大值$\sqrt{3}$.
故选:B.
点评 本题考查向量的数量积的定义和性质,以及向量的数量积的坐标表示,以及不等式的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1,p2 | B. | p3,p4 | C. | p2,p3 | D. | p1,p4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
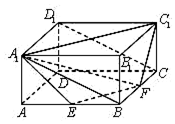 如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点,证明A1,C1,F,E四点共面,并求点B到平面A1EF的距离.
如图,在长方体ABCD-A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点,证明A1,C1,F,E四点共面,并求点B到平面A1EF的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com