练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝x|x|－2x，则下列结论正确的是(　　)

    A．f(x)是偶函数，递增区间是(0，＋∞)

    B．f(x)是偶函数，递减区间是(－∞，1)

    C．f(x)是奇函数，递减区间是(－1,1)

    D．f(x)是奇函数，递增区间是(－∞，0)


    C　将函数f(x)＝x|x|－2x去掉绝对值得f(x)＝画出函数f(x)的图像，如图，观察图像可知，函数f(x)的图像关于原点对称，故函数f(x)为奇函数，且在(－1,1)上单调递减．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    有下列几个命题：

    ①“若a>b，则a2>b2”的否命题；

    ②“若x＋y＝0，则x，y互为相反数”的逆命题；

    ③“若x2<4，则－2<x<2”的逆否命题．

    其中真命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)定义在R上，f(2－x)＝f(x)，且当x≥1时，f(x)＝ln x，则有(　　)

    A．f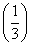<f(2)<f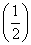

    B．f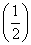<f(2)<f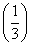

    C．f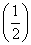<f<f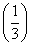(2)

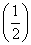    D．f(2)<f<f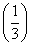

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设，若仅有一个常数c使得对于任意的，都有满足方程，这时，的取值的集合为                  。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中，从极点O作直线与另一直线相交于点M，在OM上取一点P，使．

    （1）求点P的轨迹方程；（2）设R为上任意一点，试求RP的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)是(－∞，＋∞)上的奇函数，f(x＋2)＝－f(x)，

    当0≤x≤1时，f(x)＝x.

    (1)求f(3)的值；

    (2)当－4≤x≤4时，求f(x)的图像与x轴所围成图形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝的图像大致是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知幂函数f(x)＝x(m2＋m)－1(m∈N*)，经过点(2，)，试确定m的值，并求满足条件f(2－a)>f(a－1)的实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某电视新产品投放市场后第一个月销售100台，第二个月销售200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好地反映销量y与投放市场的月数x之间关系的是(　　)

    A．y＝100x　　　　　　                     B．y＝50x2－50x＋100

    C．y＝50×2x                                      D．y＝100log2x＋100

    查看答案和解析>>

    同步练习册答案