
| 投入资金 | 甲产品利润 | 乙产品利润 |
| 4 | 1 | 2.5 |
| A. | $\frac{9}{2}$ | B. | $\frac{65}{16}$ | C. | $\frac{35}{8}$ | D. | $\frac{17}{4}$ |
分析 根据条件求出甲乙产品的利用表达式,分别求出投入甲乙两种产品的销售获得利润,利用换导数法求出最大值.
解答 解:∵甲产品的利润与投入资金成正比,
∴设y=kx,当投入4万时,利润为1,即4k=1,得k=$\frac{1}{4}$,即y=$\frac{1}{4}$x,
∵乙产品的利润与投入资金的算术平方根成正比,
∴设y=k$\sqrt{x}$,当投入4万时,利润为2.5=$\frac{10}{4}$=$\frac{5}{2}$,即$\sqrt{4}$k=$\frac{5}{2}$,得2k=$\frac{5}{2}$,
即k=$\frac{5}{4}$,即y=$\frac{5}{4}$$\sqrt{x}$,
设乙产品的投入资金x,则甲产品投入资金10-x,0≤x≤10,
则销售甲乙产品所得利润y=$\frac{1}{4}$(10-x)+$\frac{5}{4}$$\sqrt{x}$,
则函数的导数y′=-$\frac{1}{4}$+$\frac{5}{8\sqrt{x}}$=$\frac{5-2\sqrt{x}}{8\sqrt{x}}$,
由f′(x)>0得5-2$\sqrt{x}$>0,即0<x<$\frac{25}{4}$,
由f′(x)<0得5-2$\sqrt{x}$<0,即x>$\frac{25}{4}$,
即当x=$\frac{25}{4}$时,函数取得极大值同时也是最大值,此时f($\frac{25}{4}$)=$\frac{1}{4}$(10-$\frac{25}{4}$)+$\frac{5}{4}$$•\sqrt{\frac{25}{4}}$=$\frac{15}{16}$+$\frac{50}{16}$=$\frac{65}{16}$,
故选:B
点评 本题主要考查了函数模型的选择与应用,以及函数的最值的求解,利用导数法是解决本题的关键.,考查学生的运算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
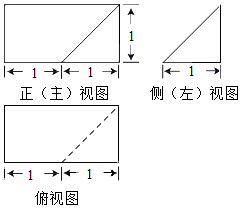
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
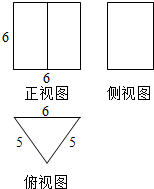 某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120.
某几何体的三视图如图所示,其中正视图是边长为6的正方形,俯视图是腰长为5,底边长为6的等腰三角形,则该几何体的体积是72,表面积是120.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
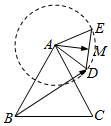 如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )
如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{4}$+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{4}$ | D. | $\frac{3}{4}$+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com