
分析 (Ⅰ)依题意$\left\{\begin{array}{l}{a^2}={b^2}+{c^2}\\ bc=1\\ b=c\end{array}\right.$解得$\left\{\begin{array}{l}a=\sqrt{2}\\ b=1\end{array}\right.$,即可得椭圆方程;
(Ⅱ)设过椭圆右焦点F2的直线CD为x=ty+1,C(x1,y1),D(x2,y2),则$\left\{\begin{array}{l}x=ty+1\\{x^2}+2{y^2}=2\end{array}\right.$整理得(t2+2)y2+2ty-1=0,可得$|{y_1}-{y_2}|=\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}=\frac{{\sqrt{8{t^2}+8}}}{{{t^2}+2}}=\frac{{2\sqrt{2}\sqrt{{t^2}+1}}}{{{t^2}+2}}$,
S四边形ABCD=$4{S_{△OCD}}=\frac{{4\sqrt{2}•\sqrt{{t^2}+1}}}{{{t^2}+2}}$,令$m=\sqrt{1+{t^2}}≥1$,则$S=f(m)=\frac{{4\sqrt{2}m}}{{{m^2}+1}}=\frac{{4\sqrt{2}}}{{m+\frac{1}{m}}}$,可得四边形ABCD的面积最大值.
解答 解:(Ⅰ)依题意$\left\{\begin{array}{l}{a^2}={b^2}+{c^2}\\ bc=1\\ b=c\end{array}\right.$解得$\left\{\begin{array}{l}a=\sqrt{2}\\ b=1\end{array}\right.$
即椭圆C的方程为$\frac{x^2}{2}+{y^2}=1$.
(Ⅱ)显然直线AB,CD的斜率不为0,设过椭圆右焦点F2的直线CD为x=ty+1,C(x1,y1),D(x2,y2).
则$\left\{\begin{array}{l}x=ty+1\\{x^2}+2{y^2}=2\end{array}\right.$整理得(t2+2)y2+2ty-1=0,显然△>0
∴${y_1}+{y_2}=\frac{-2t}{{{t^2}+2}}$,${y_1}{y_2}=\frac{-1}{{{t^2}+2}}$,
∴$|{y_1}-{y_2}|=\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}=\frac{{\sqrt{8{t^2}+8}}}{{{t^2}+2}}=\frac{{2\sqrt{2}\sqrt{{t^2}+1}}}{{{t^2}+2}}$,
s△OCD=${s}_{△O{F}_{2}C}+{s}_{△O{F}_{2}D}$=$\frac{1}{2}$|OF|×|y1-y2|=$\frac{\sqrt{2}•\sqrt{{t}^{2}+1}}{{t}^{2}+2}$,
∵AB∥CD,且分别过椭圆左右焦点,所以四边形ABCD为平行四边形,且O为四边形ABCD的中心S四边形ABCD=$4{S_{△OCD}}=\frac{{4\sqrt{2}•\sqrt{{t^2}+1}}}{{{t^2}+2}}$,
令$m=\sqrt{1+{t^2}}≥1$,则$S=f(m)=\frac{{4\sqrt{2}m}}{{{m^2}+1}}=\frac{{4\sqrt{2}}}{{m+\frac{1}{m}}}$,
注意到S=f(m)在[1,+∞)上单调递减,所以${S_{max}}=f(1)=2\sqrt{2}$,
当且仅当m=1,即t=0时等号成立,故这个四边形ABCD的面积最大值为$2\sqrt{2}$.
点评 本题考查了椭圆的方程,椭圆与直线的位置关系,方程思想、韦达定理,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
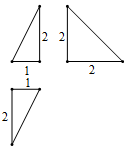 已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )
已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线的成角余弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N={x|x<3} | B. | M∩N={x|2<|x|<3} | C. | M∩N={x|2<x<3} | D. | M∪N=R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )
把一个皮球放入如图所示的由8根长均为20cm的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的半径为( )| A. | l0$\sqrt{3}$cm | B. | 10 cm | C. | 10$\sqrt{2}$cm | D. | 30cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com